
Two discs which are rotating about their respective axis of rotation with angular speed $2rad{{s}^{-1}}$and $5rad{{s}^{-1}}$ are brought in contact such that their axes of rotation will coincide. Now the angular speed of the system becomes $4rad{{s}^{-1}}$. If the moment of inertia of the second disc is $1\times {{10}^{-1}}kg{{m}^{2}}$, then what will be the moment of inertia of the first disc (in$kg{{m}^{2}}$)?
$\begin{align}
& A.0.25\times {{10}^{-3}} \\
& B.1.5\times {{10}^{-3}} \\
& C.1.25\times {{10}^{-3}} \\
& D.0.75\times {{10}^{-3}} \\
& E.0.5\times {{10}^{-3}} \\
\end{align}$
Answer
233.1k+ views
Hint: Here, first the two discs are rotating individually, and then the axis of rotation will have coincided. The angular momentum is considered. So the law of conservation of angular momentum is used in the solution to find ${{I}_{1}}$. This will help you in answering this question.
Complete step-by-step solution
Here it is given that there are two discs rotating about their respective axis of rotation with their angular speeds ${{\omega }_{1}}$and ${{\omega }_{2}}$respectively.
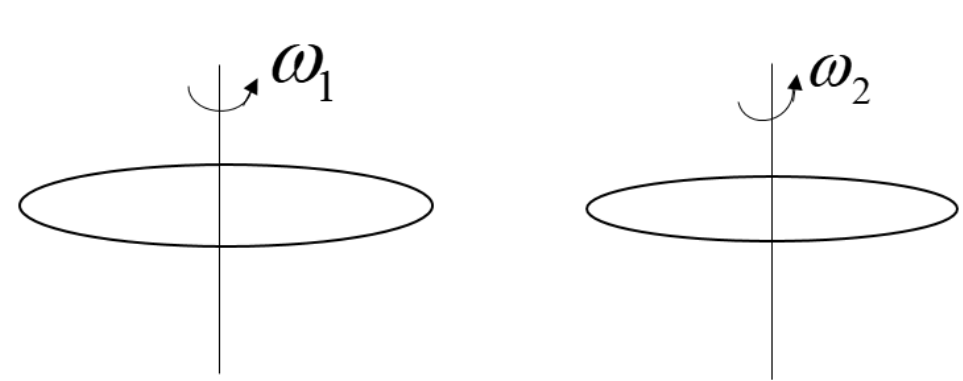
${{I}_{2}}$ will be representing the moment of inertia of second disc $=1\times {{10}^{-1}}kg{{m}^{2}}$
${{\omega }_{1}}$ will be representing the angular speed of the first disc $=2rad{{s}^{-1}}$
${{\omega }_{2}}$ will be representing the angular speed of the second disc $=5rad{{s}^{-1}}$
Now, when the two discs are brought into contact with each other such that their axes of rotation coincide together. Now the two discs will be rotating as a system with a new angular speed.
${{\omega }_{3}}$ will be representing the angular speed of system $=4rad{{s}^{-1}}$
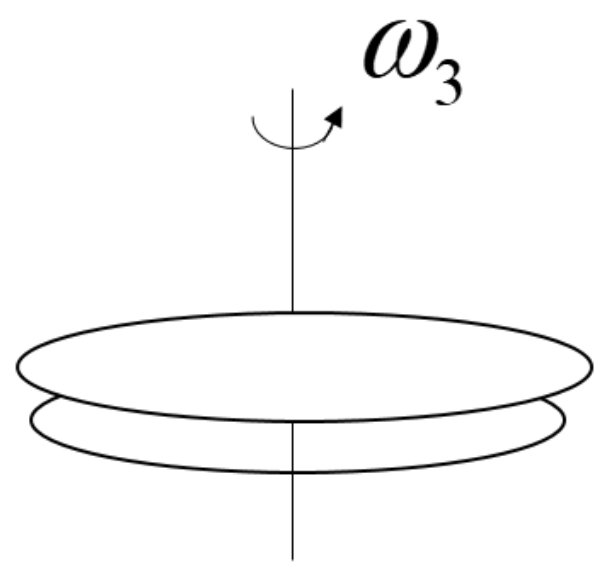
Now to find the moment of inertia of the first disc we will use the law of conservation of angular momentum.
Now the formula of angular momentum can be shown as,
$L={{L}_{1}}+{{L}_{2}}$
Where ${{L}_{1}}$ will be the angular momentum of disc one, ${{L}_{2}}$ be the angular momentum of the second one, $L$ be the angular momentum of the system.
$\begin{align}
& L={{L}_{1}}+{{L}_{2}} \\
& \Rightarrow \left( {{I}_{1}}+{{I}_{2}} \right){{\omega }_{3}}={{I}_{1}}{{\omega }_{1}}+{{I}_{2}}{{\omega }_{2}} \\
\end{align}$
Let us substitute the values we know from the question in this,
$\begin{align}
& \Rightarrow \left( {{I}_{1}}+1\times {{10}^{-1}} \right)\times 4={{I}_{1}}\times 2+1\times {{10}^{-1}}\times 5 \\
& \Rightarrow 4{{I}_{1}}+4\times {{10}^{-1}}=2{{I}_{1}}+5\times {{10}^{-1}} \\
\end{align}$
Rearranging the equation can be shown as,
$\begin{align}
& \Rightarrow 4{{I}_{1}}-2{{I}_{1}}=5\times {{10}^{-1}}-4\times {{10}^{-1}} \\
& \Rightarrow 2{{I}_{1}}=1\times {{10}^{-1}} \\
\end{align}$
Hence the current will be,
${{I}_{1}}=0.5\times {{10}^{-1}}kg{{m}^{2}}$
Therefore the moment of inertia of the first disc has been obtained. The correct answer has been mentioned as option E.
Note: Here when the two discs coincide about their axis of rotation angular momentum is conserved. The angular velocity of the system decreases after coinciding. The angular velocity of the system decreases after coinciding together with the axis.
Complete step-by-step solution
Here it is given that there are two discs rotating about their respective axis of rotation with their angular speeds ${{\omega }_{1}}$and ${{\omega }_{2}}$respectively.
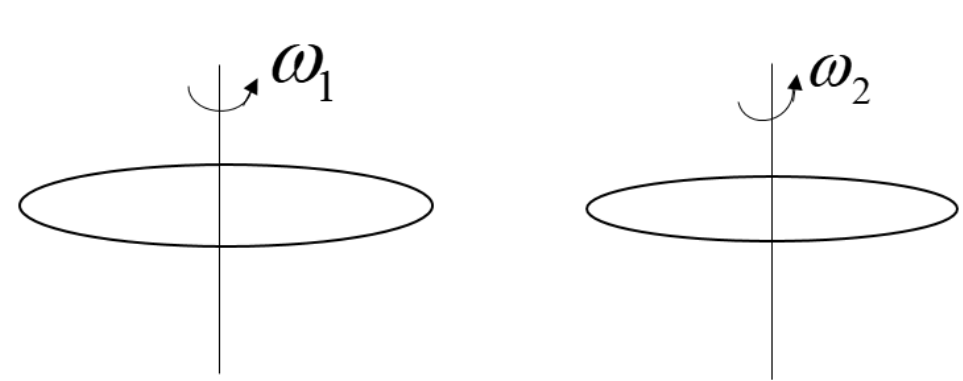
${{I}_{2}}$ will be representing the moment of inertia of second disc $=1\times {{10}^{-1}}kg{{m}^{2}}$
${{\omega }_{1}}$ will be representing the angular speed of the first disc $=2rad{{s}^{-1}}$
${{\omega }_{2}}$ will be representing the angular speed of the second disc $=5rad{{s}^{-1}}$
Now, when the two discs are brought into contact with each other such that their axes of rotation coincide together. Now the two discs will be rotating as a system with a new angular speed.
${{\omega }_{3}}$ will be representing the angular speed of system $=4rad{{s}^{-1}}$

Now to find the moment of inertia of the first disc we will use the law of conservation of angular momentum.
Now the formula of angular momentum can be shown as,
$L={{L}_{1}}+{{L}_{2}}$
Where ${{L}_{1}}$ will be the angular momentum of disc one, ${{L}_{2}}$ be the angular momentum of the second one, $L$ be the angular momentum of the system.
$\begin{align}
& L={{L}_{1}}+{{L}_{2}} \\
& \Rightarrow \left( {{I}_{1}}+{{I}_{2}} \right){{\omega }_{3}}={{I}_{1}}{{\omega }_{1}}+{{I}_{2}}{{\omega }_{2}} \\
\end{align}$
Let us substitute the values we know from the question in this,
$\begin{align}
& \Rightarrow \left( {{I}_{1}}+1\times {{10}^{-1}} \right)\times 4={{I}_{1}}\times 2+1\times {{10}^{-1}}\times 5 \\
& \Rightarrow 4{{I}_{1}}+4\times {{10}^{-1}}=2{{I}_{1}}+5\times {{10}^{-1}} \\
\end{align}$
Rearranging the equation can be shown as,
$\begin{align}
& \Rightarrow 4{{I}_{1}}-2{{I}_{1}}=5\times {{10}^{-1}}-4\times {{10}^{-1}} \\
& \Rightarrow 2{{I}_{1}}=1\times {{10}^{-1}} \\
\end{align}$
Hence the current will be,
${{I}_{1}}=0.5\times {{10}^{-1}}kg{{m}^{2}}$
Therefore the moment of inertia of the first disc has been obtained. The correct answer has been mentioned as option E.
Note: Here when the two discs coincide about their axis of rotation angular momentum is conserved. The angular velocity of the system decreases after coinciding. The angular velocity of the system decreases after coinciding together with the axis.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Uniform Acceleration in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




