Class 4 Maths Chapter 9 Equal Groups NCERT Solutions

Class 4 Maths Chapter 9 Equal Groups Question Answer Solutions

NCERT Textbook Pages 128-130 Animal Jumps

Fill in the blank spaces with the appropriate numbers. Find how many jumps the animal needs to take to reach its food.

Question 1. The frog jumps 3 steps at a time. Which numbers will the frog touch? Will it touch 67?        

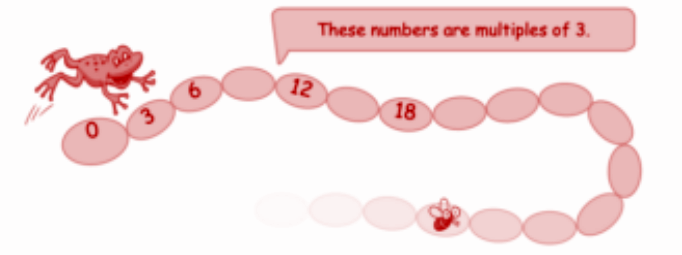
Solution:

The frog will touch the numbers that are multiples of 3, such as 0, 3, 6, 9, and so on. However, 67 is not a multiple of 3, so the frog will not touch the number 67.

Question 2. The squirrel jumps 4 steps at a time. Which numbers will the squirrel touch? How many times should the squirrel jump to reach 60?

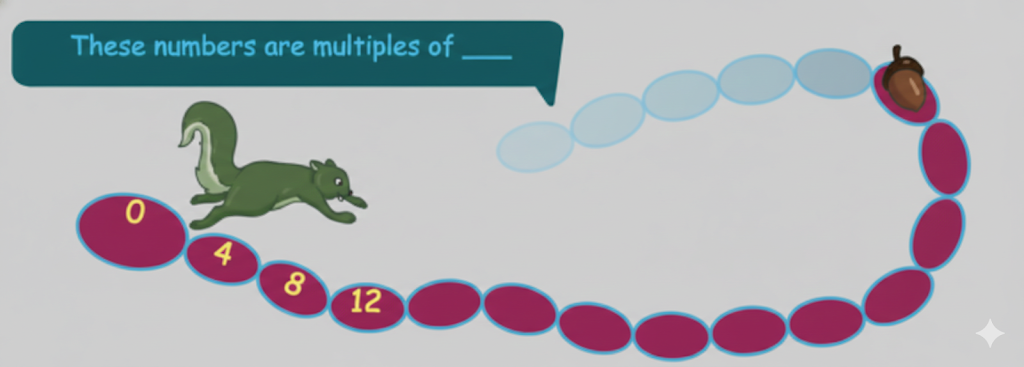
Solution:

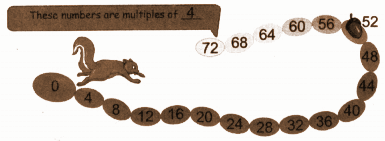
The squirrel touches the numbers 0, 4, 8, 12, and so on, which are multiples of 4.

Since the squirrel jumps 4 steps at a time, and we know that 4 × 15 = 60,
the squirrel needs to jump 15 steps to reach 60.

Question 3. The rabbit jumps 6 steps at a time. Which numbers will the rabbit touch? What is the smallest 3-digit number on which the rabbit will land? How many times did the rabbit jump to reach this number?

Solution:

The rabbit will touch the numbers 0, 6, 12, 18, 24, and so on, which are multiples of 6.

Since 6 × 16 = 96 and 6 × 17 = 102,
the smallest 3-digit number the rabbit will land on is 102.

Thus, the rabbit will have jumped 17 times to reach the number 102.

Question 4. The kangaroo jumps 8 steps at a time. Which numbers will the kangaroo touch?

Are there numbers that both the rabbit and the kangaroo will touch?

Solution:

The kangaroo touches the numbers 0, 8, 16, 24, and so on, which are multiples of 8.

The rabbit touches the numbers 0, 6, 12, 18, 24, and so on, which are multiples of 6.

Therefore, both the rabbit and the kangaroo will land on common numbers, such as 24, 48, 72, and so on.

Question 5. To reach 48, how many times did the rabbit jump?

How many times did the Kangaroo jump to reach the same number?

What did you observe? Share your thoughts,

Solution: 

Since the rabbit jumps 6 steps at a time, 6 steps × 8 = 48, meaning the rabbit jumped 8 times to reach 48.

The kangaroo, on the other hand, jumps 8 steps at a time, 8 steps × 6 = 48, so the kangaroo jumped 6 times to reach 48.

This shows that, due to its smaller steps, the rabbit takes more jumps than the kangaroo and thus reaches the number later.

Question 6. To reach 60, how many times did the frog jump? How many times did the rabbit jump to reach the same number?

What do you observe? Share your thoughts.

Solution:

Since the frog jumps 3 steps at a time, 3 steps × 20 = 60, meaning the frog jumped 20 times to reach 60.

The rabbit, however, jumps 6 steps at a time, 6 steps × 10 = 60, so the rabbit jumped 10 times to reach 60.
This shows that due to the difference in jump size, the frog needs to take more steps than the rabbit to reach 60.

Question 7. If the cat and the rat land on the same number, the cat will catch the rat. The cat is now on 6 and the rat on 12. When the cat jumps 3 steps forward, the rat jumps 2 steps forward. Will the cat catch the rat? If yes, at which number?

Solution:

The cat will jump on the numbers 6, 9, 12, 15, 18, 21, 24, 27, and so on.

The rat will jump on the numbers 12, 14, 16, 18, 20, 22, 24, 26, 28, and so on.

On their 6th jump, both the cat and the rat will land on 24. Therefore, the cat will catch the rat at 24.

Question 8. Find multiplication and division sentences below. Shade the sentences. How many can you find? Two examples are done for you.

Solution:

We can make 15 such sentences.

NCERT Textbook Page 130 – Common Multiples

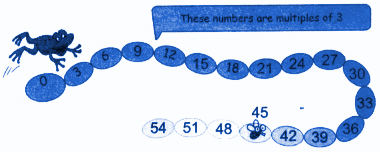
Question 1. Which numbers do both the frog and the squirrel touch? A few common multiples of 3 and 4 are

Solution:

The frog touches the numbers 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, and so on.

The squirrel touches the numbers 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, and so on.

Therefore, both the frog and the squirrel land on the common numbers 12, 24, 36, 48, and so on.

Thus, the common multiples of 3 and 4 are 12, 24, 36, 48, and so on.

Question 2. Which numbers do both the rabbit and the kangaroo touch? A few common multiples of 6 and 8 are .

Solution:

The rabbit touches the numbers 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, and so on.

The kangaroo touches the numbers 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, and so on.

Both the rabbit and the kangaroo land on the common numbers 24, 48, 72, 96, and so on.

Thus, the common multiples of 6 and 8 are 24, 48, 72, 96, and so on.

NCERT Textbook Pages 131-133 Gulabo’s Garden

Question 1. Gulabo’s garden has lily flowers. Each lily flower has 3 petals.

How many petals are there in 12 flowers? Show how you found your answer.

Gulabo will have 12 × 3 petals.

Petals in 10 lilies = 10 × 3 petals = 30 petals

Petals in 2 lilies = _______________________

Petals in 12 lilies = _______________________

Solution:
Gulabo will have 12 × 3 petals.
The total number of petals in 10 lilies is:
10 × 3 petals = 30 petals.
The total number of petals in 2 lilies is:
2 × 3 petals = 6 petals.
The total number of petals in 12 lilies is:

12 × 3 petals = 36 petals.

Question 2. In a hibiscus flower there are 5 petals. Gulabo counted all the petals and found them to be 80. How many flowers did she have?

Gulabo has 80 ÷ 5 flowers.

5 petals is 1 flower.

10 petals are 2 flowers.

50 petals are 10 flowers.

Then, 80 petals are _______ flowers.

Solution: 80 petals are 80 ÷ 5 = 16 flowers.

Question 3. Gulabo plants some marigold saplings in a box as shown in the picture.

There are _______ saplings in each row.

There are _______ rows.

How many saplings has she planted? How did you calculate it?

Mathematical Statement _______

Solution:
There are 11 saplings in each row, and there are 3 rows.
Gulabo has planted a total of 33 saplings in the box.

By using multiplication, we calculated the number of saplings.

Mathematical statement: There are 3 rows in the box, and each row contains 11 saplings.

Thus, the total number of saplings planted is:
3 × 11 = 33.

Question 4. “Dailyfresh” supermarket has kept boxes of strawberries in a big tray.

How many boxes of strawberries does the supermarket have?

Show how you found them.

There are _______ columns of strawberry boxes.

There are _______ boxes in each column.

There are _______ boxes in all.

Mathematical Statement _______

Solution:

There are 16 columns of strawberry boxes, with 6 boxes in each column.
In total, there are 96 boxes.

Mathematical statement:
The total number of strawberry boxes is calculated by multiplying the number of columns by the number of boxes in each column:
16 × 6 boxes = 96 boxes.

Question 5. Radha runs a bakery shop. She bakes 18 cupcakes in one tray of the size shown below,

(a) Complete arranging the cupcakes in the two trays given below.

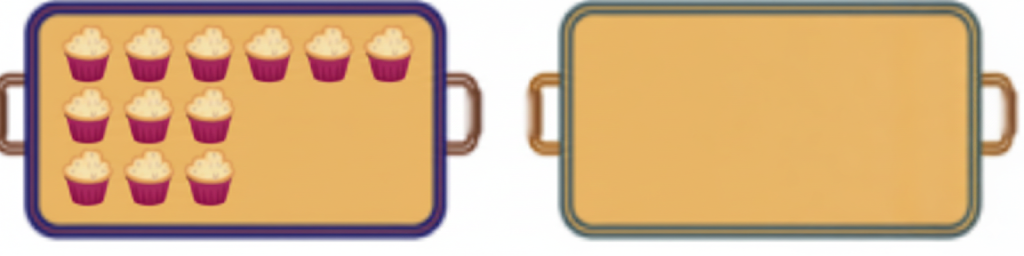
Solution:

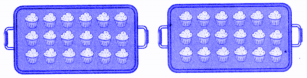
(b) She can use two such trays in her oven at a time. How many cupcakes can she make in one attempt? _______

Solution:

The number of cupcakes in one tray is 18.

The number of cupcakes in two trays is:
2 × 18 = 36.

Therefore, the total number of cupcakes she can make in one attempt is 36.

(c) Today she has received a special order. She has made 108 cupcakes. How many trays has she baked?

Solution:

The number of cupcakes in two trays is 36.

The number of cupcakes in 4 trays is:
2 × 36 = 72.

The number of cupcakes in 6 trays is:
3 × 36 = 108.

Therefore, the required number of trays is 6.

(d) She has another square baking tray. She can bake 36 mini cupcakes in such a tray. Complete the arrangement below.

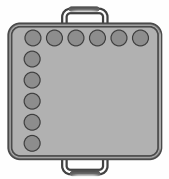
Number of columns: _______________________

Number of cup cakes in each column: _______________________

Multiplication statement _______

Find different ways for arranging the following numbers of cupcakes in rows and columns in your notebook.

36, 8, 12, and 24

Solution: 

The number of columns is 6, and the number of cupcakes in each column is 6.

Multiplication statement:
6 × 6 = 36, meaning there are 36 cupcakes. These can also be arranged in a tray with 9 rows, where each row contains 4 cupcakes.

Similarly,

• 8 cupcakes can be arranged in 4 columns, with 2 cupcakes in each column.

• 12 cupcakes can be arranged in 2 rows, with 6 cupcakes in each row.

• 24 cupcakes can be arranged in 6 columns, with 4 cupcakes in each column.

NCERT Textbook Pages 133-136 The Doubling Magic

Magician Anvi came one day,
To Gulabo’s house, ready to play.
From her coat, with a grand display,

How many flowers are there now? ___

Solution:
46

Solution:

What magic did Anvi do?

a) Double of 32 =_____
b) Double of 14 =_____
c) Double of 26 =_____
d) Double of 17 =_____
e) Double of 39 =_____
f) Double of 45 =_____

Solution:
Magician Anvi makes the flowers double after her magic.

(a) Double of 32 = 64
(b) Double of 14 = 28
(c) Double of 26 = 52
(d) Double of 17 = 34
(e) Double of 39 = 78
(f) Double of 45 = 90

Question 1. Guess what will be the ones digit of the following numbers when doubled.
Write the ones digit in the space provided,
a) 28 ______ b) 56 ______ c) 45 ______ d) 17 ______

Solution:
(a) 6
(b) 2
(c) 0
(d) 4

Question 2. Give examples of numbers that when doubled give the following digits in the ones place,

a) 0 _______
b) 2 _______
c) 4 _______
d) 6 _______
e) 8 _______

Solution:
(a) 5
(b) 2 6
(c) 2
(d) 8
(e) 4

What do we noticfe about the numbers that we get after doubling? Even or Odd?

Solution:

Doubling is an arithmetic operation, which means multiplying a number by 2. When we double any number, the result is always an even number.

Can we get 3, 5, 7, 9 as the ones digit after doubling?

Solution: Since doubling any number always results in an even number, we cannot have 3, 5, 7, or 9 as the ones digit after doubling a number.

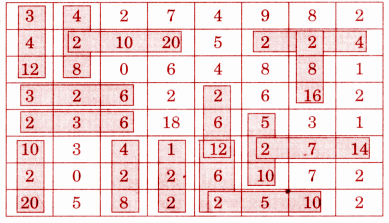
Fill each square in the chart by multiplying the row number by the column number.

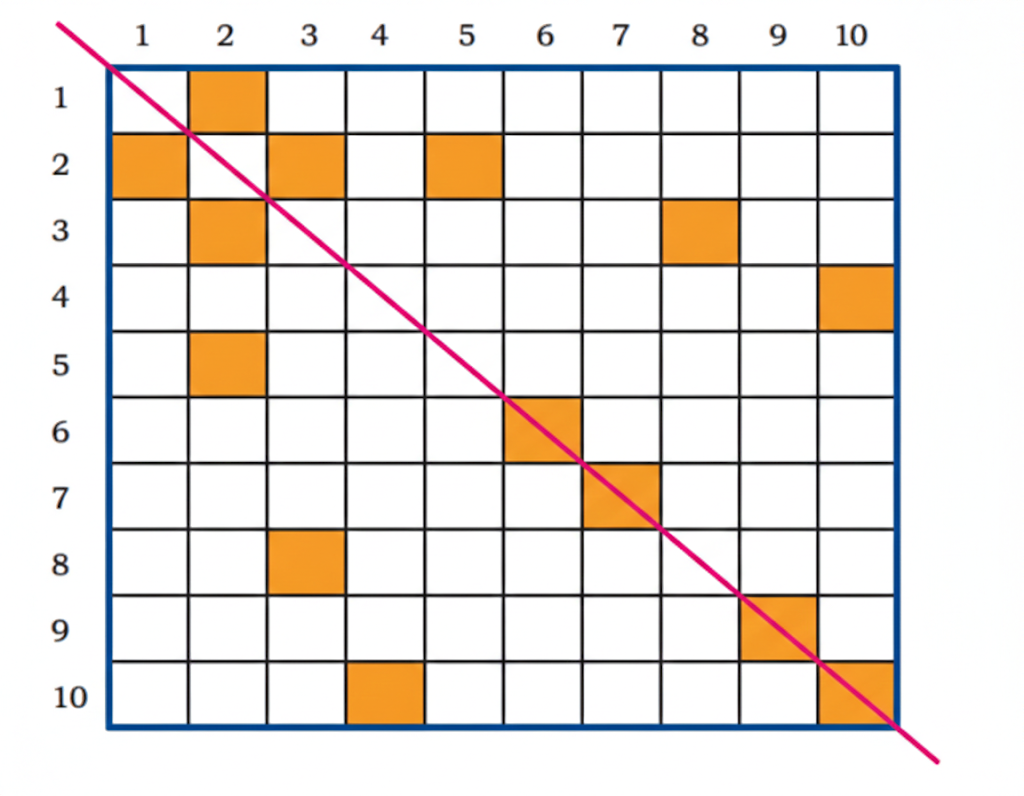
Solution:

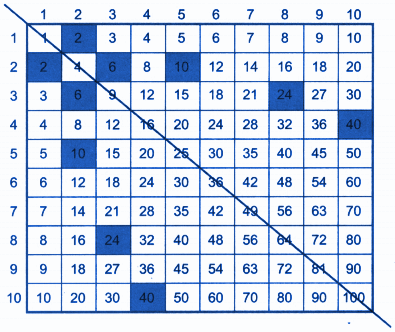
What do you notice about the numbers shaded in green? Why is this happening?

Solution:

We observe that the numbers shaded in green demonstrate that the order of multiplication does not affect the result. For instance, 1 × 2 = 2 = 2 × 1, 2 × 3 = 6 = 3 × 2, 5 × 2 = 10 = 2 × 5, and so on.

What do you notice about the numbers shaded in green? Why is this happening?

Solution: The numbers shaded in green highlight that the order of multiplication does not affect the result. For example, 1 × 2 = 2 = 2 × 1, 2 × 3 = 6 = 3 × 2, 5 × 2 = 10 = 2 × 5, and so on.

Question 1. Share the patterns that you notice in the table.

Solution: We observe that each row and column is a multiple of its respective row or column number. Additionally, the diagonal cells contain only perfect squares.

Question 2. Are the numbers in row 7 the same as the numbers in column 7? In general, are the numbers in a given row the same as the numbers in the corresponding column? Why does this happen?

Solution: Yes, in multiplication, the order of the numbers doesn't affect the product; the result remains the same regardless of the order.

Question 3. Is there a row where all answers (products) are even numbers? Which rows have this property?

Solution: Yes, there are rows where all the products are even numbers. The rows for 2, 4, 6, 8, and 10 consist entirely of even products.

Question 4. Is there a row having only odd numbers as products?

Solution: No.

Question 5. Are there rows that have both even and odd numbers? What do you notice? Why is it so?

Solution: Yes, the rows for 1, 3, 5, 7, and 9 include both even and odd numbers. This happens because multiplying an odd number by an even number produces an even result, while multiplying two odd numbers results in an odd number.

Question 6. Are there more even numbers in the chart or odd numbers? How do you know?

Solution: The chart contains more even numbers because the tables of 2, 4, 6, 8, and 10 consist entirely of even numbers.

Question 7. Colour the common multiples of the following numbers. Use different colours for each item.

(a) 2 and 3

(b) 4 and 8

(c) 7 and 9

Share your observations regarding the numbers that are common multiples in each case.

Solution: 

(a) The common multiples of 2 and 3 are 6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, and 96.

These common multiples are the multiples of 6, which is the product of 2 and 3.

(b) The common multiples of 4 and 8 are 8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, and 96.
The common multiples of 4 and 8 are the multiples of 8, which is itself a multiple of 4.

(c) The common multiple of 7 and 9 is 63.

The first common multiple of 7 and 9 is 63, which is a multiple of both.

Question 8. Observe the pattern in the ones digit of the products in row 5?

Observe the ones digit of the products in other rows also. What patterns do you notice?

Solution:  We notice that the ones digits in the products of row 5 are only 0 and 5.
Additionally, we observe other patterns in the ones digits of the products in the other rows. For example, the ones digits in row 1 are the counting numbers from 0 to 10, the ones digits in row 2 are all even numbers, and the ones digit in row 10 is always 0, and so on.

Question 9. Here is row 8 of the chart: 8, 16, 24, 32, 40, 48, 56, 64, 72, 80.

The ones digit of the products are: 8, 6, 4, 2, 0, 8, 6, 4, 2,0 .

Do’ you see a repeating pattern here?

Guess the ones digit of the following products. Verify your answer by multiplying. Write the digit in the space given.
11 × 8 = _____ 12 × 8 = _____ 13 × 8 = _____

Solution:
Yes, the pattern of ones digits is 8, 6, 4, 2, 0 and is repeating.

Since 1 × 8 = 8,

2 × 8 = 16, 3 × 8 = 24. So, the ones digits of 11 × 8, 12 × 8, and 13 × 8 are 8, 6, and 4, respectively.

11 × 8 = 88 12 × 8 = 96 13 × 8 = 104

Question 10. In row 8 of the chart, there is no number whose ones digit is 1. What other digits do not appear as the ones digit?

Solution: The digits 3, 5, 7, and 9 do not appear as the ones digit in row 8 of the chart.

Question 11. Is there a row in which all the digits from 0 to 9 appear as the ones digit? Which rows have this property?

Solution: Yes, rows 1, 3, 7, and 9 have this property.

Question 12. It can be seen in row 8 that 0 appears as the ones digit two times.

___ × 8 gives 0 as the ones digit.

What numbers can go in the box? Give 5 examples of such numbers.

Solution:
5 × 8 = 40 or 10 × 8 = 80, gives 0 as the ones digit.
15 × 8 = 120, 20 × 8 = 160, 25 × 8 = 200, 30 × 8 = 240, 35 × 8 = 280.

Question 13. Is there a row in which 0 appears as the ones digit only once?

Which rows have this property?

Solution: Yes, this property is found in the rows for 1, 3, 7, and 9.

Question 14. What do you notice about the answers for Questions 11 and 13? Share in the grade.

Solution: Students should do it by themselves..

NCERT Textbook Page 137 Multiples of Tens

Question 1. Let us count the number of wheels in tricycles.

Number of wheels in 10 tricycles with 3 wheels in each is 10 × 3 wheels = ______ wheels

Number of wheels in 10 more tricycles with 3 wheels in each is 10 × 3 wheels = _______ wheels.

Number of wheels in 20 tricycles with 3 wheels in each is 20 × 3 wheels = ______ + _____ = ______ wheels.

10 × 3 = _____
20 × 3 = _____

Solution:
Number of wheels in 10 tricycles with 3 wheels in each is 10 × 3 wheels = 30 wheels.

Number of wheels in 10 more tricycles with 3 wheels in each is 10 × 3 wheels = 30 wheels.

Number of wheels in 20 tricycles with 3 wheels in each is 20 × 3 wheels = 30 + 30 = 60 wheels.

10 × 3 = 30
20 × 3 = 60

Question 2. Let us count the number of wheels in cars.

Number of wheels in 10 cars with 4 wheels in each is 10 × 4 wheels = _______ wheels.

Number of wheels in 30 cars with 4 wheels in each is 30 × 4 wheels = _____ + _____ + _____ = _____ wheels.

Solution: 

The total number of wheels in 10 cars, each with 4 wheels, is:
10 × 4 = 40 wheels.

The total number of wheels in 30 cars, each with 4 wheels, is:
30 × 4 = 40 + 40 + 40 = 120 wheels.

In summary:
10 × 4 = 40
30 × 4 = 120.

Solve the following in a similar way. Share how you found the answers.

a) 10 × 6 = ____
b) 40 × 6 = ____
c) 10 × 8 = ____
d) 60 × 8 = ____
e) 6 × 8 = ____
g) 4 × 6 = ____
f) 60 × 8 = ____
h) 40 × 8 = ____

Solution:
(a) 10 × 6 = = 60
(b) 40 × 6 = = 60 + 60 + 60 + 60 = 240
(c) 10 × 8 = 80
(d) 60 × 8 = 80 + 80 + -80 + 80 + 80 + 80 = 480
(e) 6 × 8 = 48
(f) 60 × 8 = = 10 × 48 = 480
(g) 4 × 6 = 24
(h) 40 × 8 = 40 + 40 + 40 + 40 + 40 + 40 + 40 + 40 = 320

What happens when the number of groups is a multiple of 10?

Solution: If the number of groups is a multiple of 10, its ones digit will always be 0.

NCERT Textbook Page 138-139 Multiplying Using 10s

Question 1. Radha is packing cupcakes in boxes of 4. She has packed 18 boxes. How many cupcakes are there in the packed boxes?

18 boxes have 4 cupcakes in each.

So, there are 18 × 4 cupcakes.

10 boxes with 4 cupcakes in each contain

10 × 4 cupcakes = ______ cupcakes.

8 boxes with 4 cupcakes in each contain

8 × 4 cupcakes = _________ cupcakes.

18 boxes with 4 cupcakes in each contain

____ + ____ cupcakes

= _________ cupcakes.

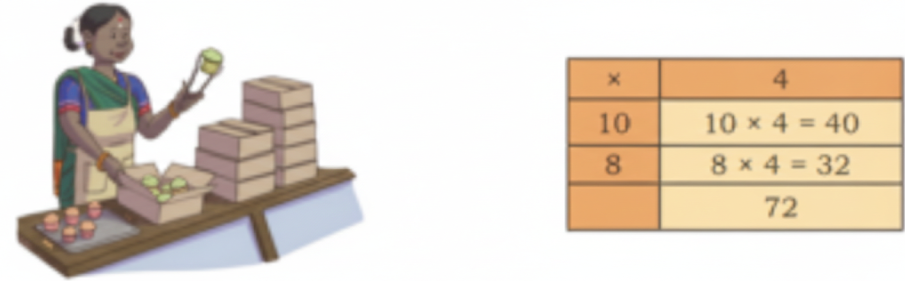
Solution:
There are 18 boxes, with 4 cupcakes in each.

Thus, the total number of cupcakes is 18 × 4.

For 10 boxes, each containing 4 cupcakes:
10 × 4 = 40 cupcakes.

For 8 boxes, each containing 4 cupcakes:
8 × 4 = 32 cupcakes.

Therefore, the total number of cupcakes in 18 boxes is:
40 + 32 = 72 cupcakes.

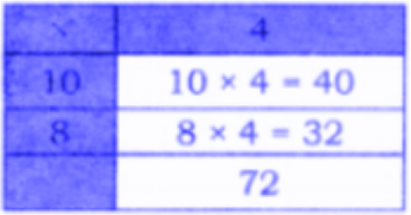
Question 2. 8 bamboo rods are needed to make a bullock cart. How many bamboo rods are needed for 23 carts?

One cart needs 8 bamboo rods. 23 carts need 23 × 8 rods.

20 carts with 8 rods in each need 20 × 8 rods = ________ rods.

3 carts with 8 rods in each need 3 × 8 rods = _________ rods

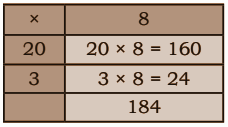
Solution:

20 carts, each with 8 rods, require 20 × 8 = 160 rods.
3 carts, each with 8 rods, require 3 × 8 = 24 rods.
Therefore, the total number of rods needed for 23 carts is:
160 + 24 = 184 rods.

NCERT Textbook Page 139 – Let Us Solve

Question 1. A flock of 25 geese and 12 sheep have gathered around a pond. Chippi the lizard sees many legs. How many legs does it see?

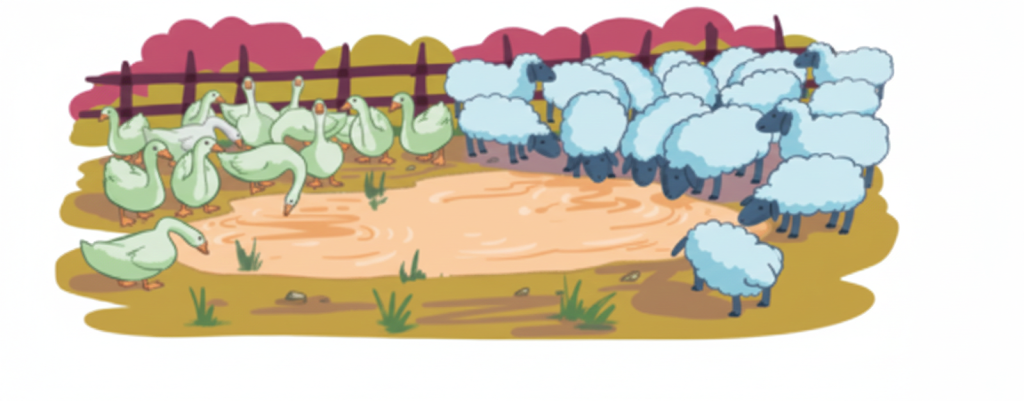
Solution:

Each goose has 2 legs, and each sheep has 4 legs.

For 25 geese: 25 × 2 = 50 legs.

For 12 sheep: 12 × 4 = 48 legs.

Therefore, the total number of legs seen by Chippi is:

50 legs + 48 legs = 98 legs.

Question 2. In an auditorium, 8 children are sitting in each row. There are 15 such rows in the school auditorium. How many children are in the auditorium?

Solution: 

There are 8 children sitting in each row.

In 15 rows, the total number of children is:
15 × 8 = 120.

Therefore, there are 120 children in the auditorium.

Question 3. A book shop has kept 9 books in each pile. There are 14 such piles. How many books does the shop have?

Solution: 

Each pile contains 9 books.

In 14 piles, there are:

14 × 9 = 126 books.

Therefore, the shop has a total of 126 books.

Question 4. Surya is making a patch work with beads of two colours as shown in the picture. How many beads has he used? How many each of golden colour  beads and white colour beads has he used in making this patch work?

Solution:
The number of columns in the patch is 8.

The number of beads in one column is:
4 × 5 = 20.

Thus, the total number of beads used by Surya is:
20 × 8 = 160.

The number of white beads in each consecutive 2 columns is 20,
so the total number of white beads in the patch is:
20 × 4 = 80.

Similarly, the number of golden beads in each consecutive 2 columns is 20,
so the total number of golden beads in the patch is:
20 × 4 = 80.

Question 5. For each of the following multiplication problems, make your own stories as above. Then find out the product.

(a) 34 × 3

(b) 75 × 5

(c) 46 × 6

(d) 50 × 9

Solution:  

(a) In a park, 3 people can sit on each bench, and there are 34 benches. To find the total number of people who can sit on the benches, we calculate:
34 × 3 = 102 people.

(b) A library has 5 books on each shelf, and there are 75 shelves. To determine the total number of books in the library, we multiply:
75 × 5 = 375 books.

(c) It takes 6 flowers to make one bouquet. To find out how many flowers are needed to make 46 bouquets, we calculate:
46 × 6 = 276 flowers.

(d) Aman is packing 9 cups in each box, and he has packed 50 boxes. To find the total number of cups in the packed boxes, we multiply:
50 × 9 = 450 cups.

(Note: These examples can be adapted to different scenarios.)

NCERT Textbook Pages 140-141 Division

Question 1. A factory has ordered 58 wheels for the small tempos that they make. Each tempo has 3 wheels.

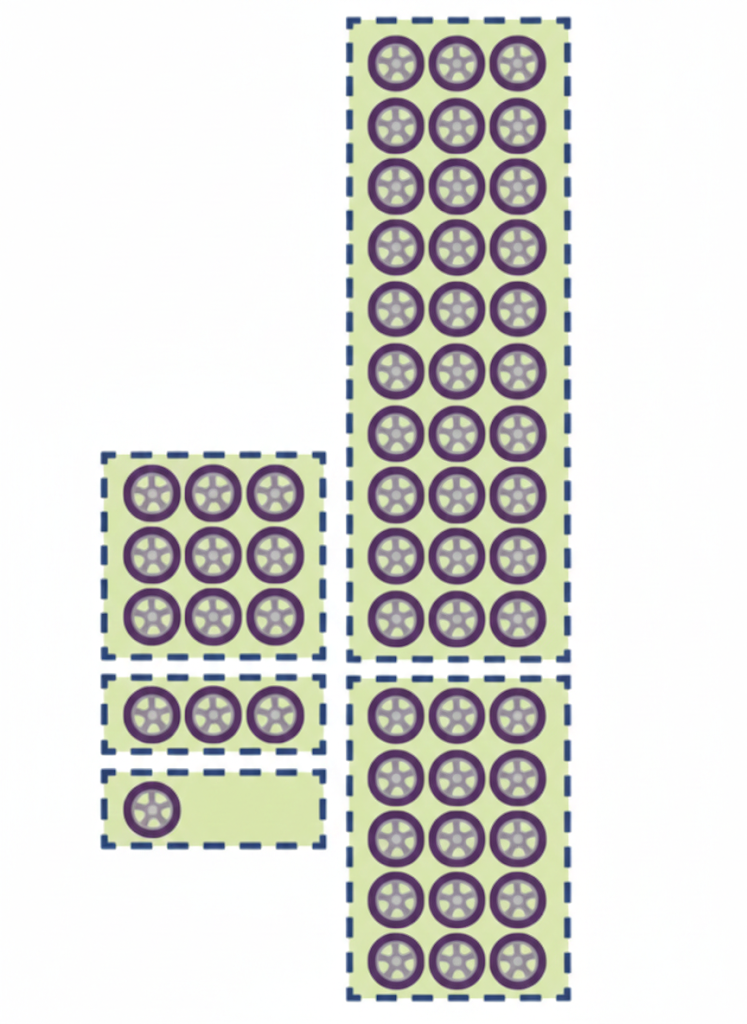
In how many tempos can they fix the wheels? Discuss your thinking in each step.

Number of tempos is 58 ÷ 3

30 wheels are needed for 10 tempos. _______wheels are left.

15 wheels are needed for _______ tempos. _______wheels are left.

9 wheels are needed for_______ tempos. _______ wheels are left.

_______ wheels are needed for_______ tempos.

_______ wheels are left

Solution:

The number of tempos is 58 ÷ 3.
For 10 tempos, 30 wheels are needed, and 28 wheels remain.
For 5 tempos, 15 wheels are needed, and 13 wheels remain.
For 3 tempos, 9 wheels are needed, and 4 wheels remain.
For 1 tempo, 3 wheels are needed, and 1 wheel remains.

Can we make another tempo?

Solution: No, because only 1 wheel is left.

Question 2. A dairy farm has many cows. Chippi the lizard is surprised to see 88 legs.

How many cows are there in the farm? Write appropriate sentences as above to show your thinking.

Number of legs of a cow: ________

Number of cows is 88 ÷ ________

Show your work using the table below.

Hint: Taking out groups of 10s is easy.

Total number of cows = ______

Solution: 

Number of legs of a cow = 4

Number of cows is 88 ÷ 4

Total number of cows = 10 + 7 + 5 

= 22

NCERT Textbook Page 141 – Let Us Solve

Question 1. In a big aquarium, Jolly fish sees 72 legs of octopuses. How many octopuses are there in the aquarium?

Solution:

Number of legs of an octopus = 8
Number of octopuses in the aquarium = 72 ÷ 8

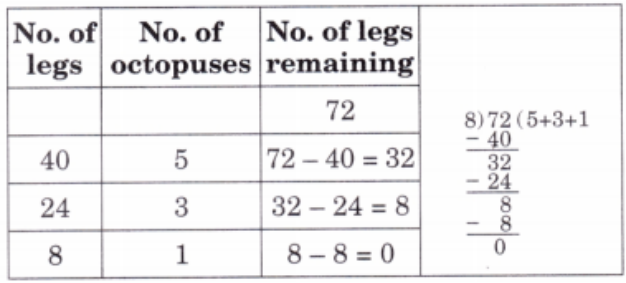
Total number of octopuses = 5 + 3 + 1 = 9.

Question 2. A sports store packs 4 shuttlecocks in a bigger box. They have 50 shuttlecocks. How many boxes will they need to pack all of them? Can they pack all the shuttlecocks in the boxes? How many are left?

Solution:

The number of shuttlecocks in one bigger box is 4.

The total number of shuttlecocks is 50.

The number of boxes required to pack all the shuttlecocks is:
50 ÷ 4.

Total number of bigger }oxes needed to pack the shuttlecocks = 10 + 2 = 12

But 12 boxes only pack 48 shuttlecocks.

Left shuttlecocks = 50 – 48 = 2

Question 3. Rakul Chachi uses a part other farm to grow flowering plants for the upcoming festive season. She has planted 75 saplings of roses. Each row has 5 saplings. How many rows of saplings has she planted?

Solution:

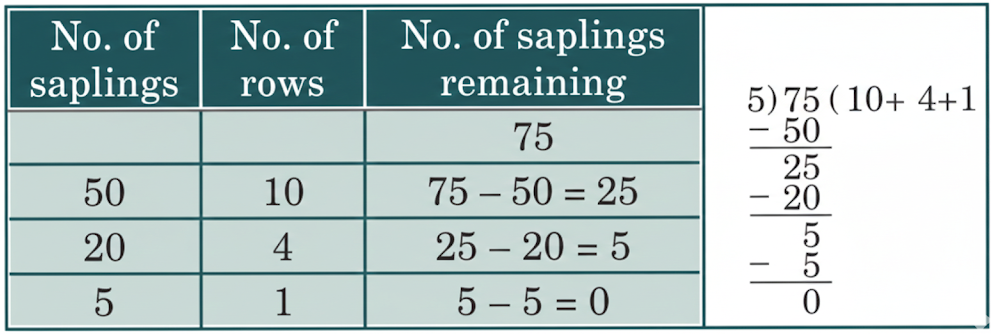
The number of saplings in each row is 5.

The number of rows of saplings planted is:
75 ÷ 5.
The total number of rows of saplings is:
10 + 4 + 1 = 15.

Question 4. Make stories for the following problems and solve them:

(a) 70 ÷ 5

Solution: Reema packs 5 balls in each box and has a total of 70 balls. To find out how many boxes she will need to pack all the balls, we calculate:
70 ÷ 5 = 14.

So, Reema will need 14 boxes to pack all the balls.

(b) 84 ÷ 7

Solution:

Rakul made 84 cupcakes for 70 + 2 children. She arranged 7 cupcakes in each row on a tray. To find out how many rows of cupcakes she arranged, we calculate:

84 ÷ 7 = 12 rows.

So, Rakul arranged 12 rows of cupcakes.

(c) 69 ÷ 3

Solution:

Mohan fixes 69 wheels for autorickshaws. To determine how many rickshaws he can fix the wheels for, assuming he fixes 3 wheels per rickshaw, we calculate:
69 ÷ 3 = 23.

So, Mohan can fix the wheels for 23 autorickshaws.

(d) 93 ÷ 6

Solution:

A group of 93 students is going on a field trip, and 6 mini buses are available. If each bus carries 3 students, we calculate how many students can go on the trip:

93 ÷ 6 = (10 + 5) = 15 students.

So, 3 students will not be able to go on the trip.

(Note: The scenario may change based on different conditions.)

NCERT Textbook Pages 142-143 – Multiples of 100

100 bikes with 2 people on each have

100 × 2 people = _____ people.

200 bikes with 2 people on each have ______people. How did you find it?

100 cars with 4 people in each have 100 × 4 people = _______ people.

500 cars with 4 people in each have ______people.

How did you find it?

Solution:

100 bikes with 2 people on each have:
100 × 2 = 200 people.

200 bikes with 2 people on each have:

200 × 2 = 100 × 2 + 100 × 2 = 200 people + 200 people = 400 people.

100 cars with 4 people in each have:

100 × 4 = 400 people.

500 cars with 4 people in each have:

500 × 4 = (100 × 4 + 100 × 4 + 100 × 4 + 100 × 4 + 100 × 4) = (400 + 400 + 400 + 400 + 400) = 2000 people.

How did you find it?

500 × 4 = _____

100 × 4 = _____

5 × 4 = _____

50 × 4 = _____

Solution:
We multiplied the number of bikes by the number of people on each bike.

500 × 4 = 2000
5 × 4 = 20
100 × 4 = 400
50 × 4 = 200

What do you notice about multiplying by multiples of 100s.

Solution:

When multiplying a number by multiples of 100, the product is obtained by multiplying the non-zero digits and adding the corresponding number of zeros from the multiple of 100.

Observe the pattern and complete the answers.

Solution:

NCERT Textbook Pages 143-144 More Multiplication

Question 1. Big electric autorickshaws run in small towns of India and can carry 8 passengers.

How many people can travel in 125 such autos in a single round?

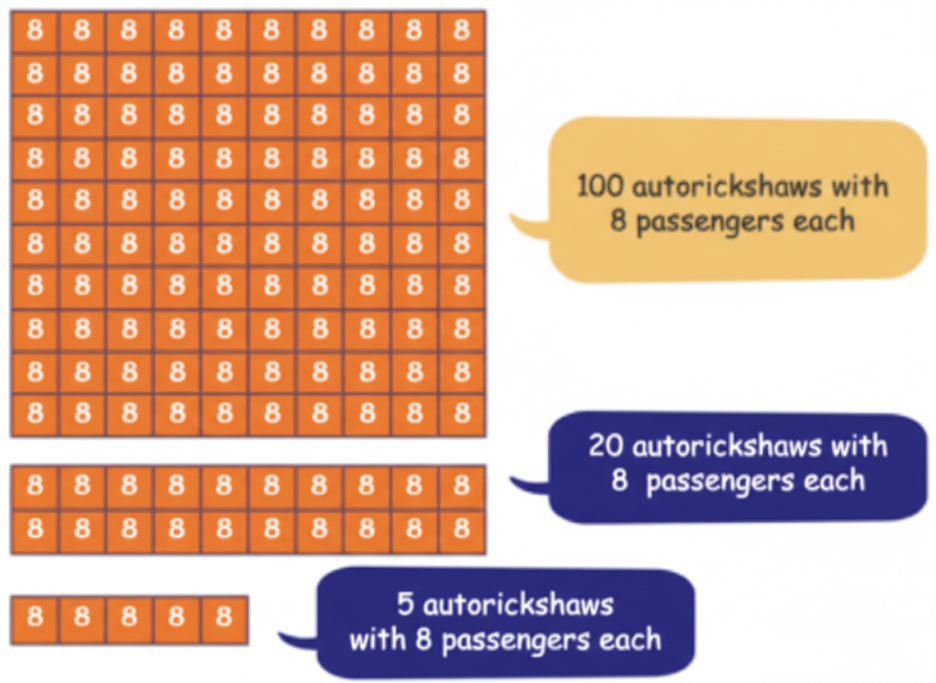
The total number of passengers 125 × 8.

100 autorickshaws with 8 passengers in each have 100 × 8 passengers = ______ passengers.

20 autorickshaws with 8 passengers in each have 20 × 8 passengers = _______ passengers.

5 autorickshaws with 8 passengers in each have 5 × 8 passengers = __________ passengers.

125 autorickshaws with 8 passengers in each have ____ + ____ + ______= _________ passengers.

Solution: 

The total number of passengers is 125.

For 100 autorickshaws, each carrying 8 passengers:
100 × 8 = 800 passengers.

For 20 autorickshaws, each carrying 8 passengers:
20 × 8 = 160 passengers.

For 5 autorickshaws, each carrying 8 passengers:
5 × 8 = 40 passengers.

Therefore, the total number of passengers in 125 autorickshaws is:
800 + 160 + 40 = 1000 passengers.

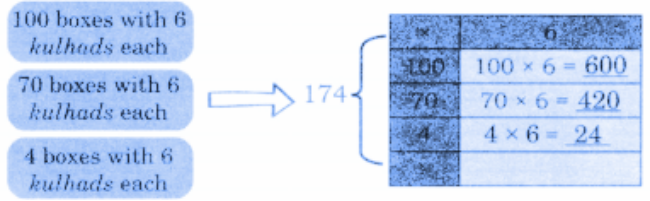
Question 2. Kahlu and Rabia are potters and make earthen pots (kulhad) for trains.

They pack 6 kulhads in a box and have packed 174 boxes for delivery. How many kulhads have they made?

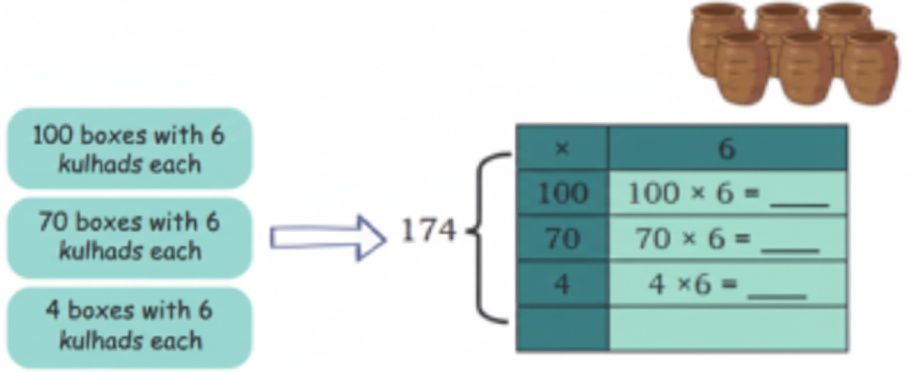
Solution:
174 × 6 = 600 + 420 + 24 = 1044

NCERT Textbook Pages 144-145 Let Us Solve

Question 1. BP Girl’s school has decided to give all its students two pencils on the first day of school. It has 465 students.

How many pencils does the school need to buy?

Solution:

The number of pencils given to each student is 2, and the total number of students is 465.

The total number of pencils the school needs to buy is:

465 × 2 = 800 + 120 + 10 = 930 pencils.

Question 2. 234 children of a school have decided to organise a school mela. Each child contributes ?5 for the organisation of the mela. How much money do they collect?

Solution:

The money contributed by each child is ₹5, and the total number of children in the school mela is 234.

The total money collected for the school mela is:
234 × ₹5.

The total money collected from 234 children, with each contributing ₹5, is:
₹1000 + ₹150 + ₹20 = ₹1170.

Question 3. Make stories for the following problems and solve them.

(a) 439 × 4

(b) 514 × 8

(c) 356 × 5

(d) 623 × 7

Solution: 

Total tickets distributed = 439 × 4

= 1600 + 120 + 36 = 1756

(b) Raman and Ishita are toymakers and make toys for children. They packed 8 toys in a box and delivered 514 boxes to a company. How many toys have they made?

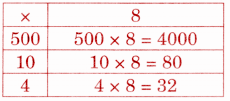
Total number of toys made = 514 × 8 = 4000 + 80 + 32

= 4112

(c) A machine packs 5 notebooks in one bundle.

If the machine packed 356 bundles, the total number of books packed is:

356 × 5 = 1500 + 250 + 30 = 1780 books.

(d) A factory has ordered 623 packets of bottles, with 7 bottles in each packet.

The total number of bottles ordered by the factory is:

623 × 7 = 4200 + 140 + 21 = 4361 bottles.

(Note: Stories may vary.)

NCERT Textbook Page 146 – Patterns in Division

How much money will each get? Draw arrows linking the money and the children to answer the questions.

1. ₹ 30 shared equally among 3 children ______________
2. ₹ 900 shared equally among 3 children ______________

Solution:
1. ₹ 30 + ₹ 3 = ₹ 10
2. ₹ 900 + ₹ 3 = ₹ 300

Using the above way of thinking, solve the following problems. Observe and explain the patterns that you notice below.

Solution:

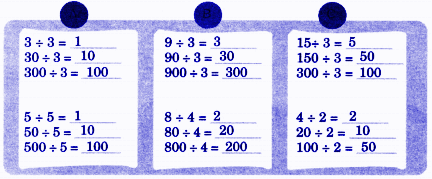
Question 1. A load carrying truck has 6 tyres. Chippi the lizard sees 60 tyres. How many trucks are there?

Solution:
Number of tyres in a truck = 6

\[

\begin{array}{r}

\phantom{-}60 \, \div \, 10 \\

\hline

60 \\

0

\end{array}

\]

The total number of tyres is 60.

The number of trucks is:
60 ÷ 6 = 10, meaning the 60 tyres are divided by 6, as each truck has 6 tyres.

Question 2. Chippi sees 80 wheels in a car parking space. How many cars are standing in the parking space?

Solution:

The number of wheels in a car is 4.

The total number of wheels in the parking space is 80.

The number of cars is:

80 ÷ 4 = 20, meaning the 80 wheels are divided by 4, as each car has 4 wheels.

Question 3. Chippi sees 600 legs of ants walking towards the anthill. How many ants are there?

Solution:

The number of legs of an ant is 6.

The total number of legs of ants walking towards the anthill is 600.

Thus, the number of ants walking towards the anthill is 600 ÷ 6 = 100 (since each ant has 6 legs).

Question 4. A fancy shop has packed 800 rubber bands in several packets. Each packet has 4 rubber bands. How many packets of rubber bands does the shop have?

Solution: 

Rubber bands in 1 packet = 4

So, Total rubber bands = 800

Thus, Number of packets of rubber bands = 800 + 4 = 200 (i.e., 800 rubber bands have been packed, with 4 rubber bands in each packet)

NCERT Textbook Pages 147-148 Let Us Solve

Question 1. A school bus hires 7 buses to take 245 children to the transport museum. Each bus carry the same number of children. How many children are traveling in each bus?

Solution:

The total number of children traveling to the museum is 245.

The school hired 7 buses.

The number of children in each bus is calculated as 245 ÷ 7 = 35 (i.e., 10 + 10 + 10 + 5 children in each bus).

Question 2. The Darjeeling Himalayan Railway is fondly called as the “Toy Train”. This toy train ride is also a UNESCO World Heritage Site.

This amazing train runs between New Jalpaiguri and Darjeeling and it also passes through one of the highest stations in the world, namely, Ghum. It runs 88 km daily. How much distance does it travel in a week?

Solution:
The "Toy Train" travels a distance of 88 km daily.

The number of days in a week is 7.

Therefore, the total distance traveled by the "Toy Train" in a week is 88 km × 7 = 616 km (which is 560 km + 56 km).

Question 3. The 16 km river rafting from Shivpuri to Rishikesh in the Ganga provides the most interesting rafting opportunity. In the summer months, VentureOut company took 259 people for rafting. Each raft can take 7 people. How many rafts did it take?

Solution:

The total number of people for rafting is 259.

Each raft accommodates 7 people.

The number of rafts required is 259 ÷ 7 = 37 (i.e., 10 + 10 + 10 + 7 rafts).

Question 4. Anu saves ₹ 45 every month by putting it in her piggy bank.

(a) How much money will Anu save in 6 months?

Solution: ₹ 45 × 6 = ₹ 40 × 6 + ₹ 5 × 6 = ₹ 240 + ₹ 30 = ₹ 270

(b) She distributes the total money saved after 6 months among 6 of her friends. How much does each friend get?

Solution: 

A total of ₹ 270 is distributed equally among 6 friends.
Therefore, the amount received by each friend is ₹ 270 ÷ 6 = ₹ 45 (i.e., ₹ 10 + ₹ 10 + ₹ 10 + ₹ 10 + ₹ 5).

(c) If she decides to distribute the saved money among 3 friends after 6 months, how much money will each get?

Solution:

The money saved by Anu in 6 months is ₹ 270.
The amount received by each of the 3 friends is ₹ 270 ÷ 3 = ₹ 90 (i.e., ₹ 10 + ₹ 10 + ₹ 10 + ₹ 10 + ₹ 10 + ₹ 10 + ₹ 10 + ₹ 10 + ₹ 10).

Question 5. Raju drives an auto in his village and takes people to the bus stand.

He makes 8 trips in a day. Which of the following questions can be exactly calculated with the above statement?

(a) How much money does he make in a day?

(b) How many trips does he make in 7 days?

(c) How much time does one trip take? *

(d) How many trips does he make in 4 weeks?

Solution: 

(a) We cannot determine how much money he earns in a day since the price per trip is not provided.

(b) The total number of trips made in 7 days is 8 trips × 7 = 56 trips.

(c) We cannot determine how much time he takes for each trip, as the time is not specified.

(d) The number of trips made in a week (7 days) is 8 × 7 = 56 trips.

The total number of trips in 4 weeks is 56 × 4 = 224 trips (which is 50 × 4 + 6 × 4 = 200 + 24).

Question 6. Solve

(a) 45 × 9

Solution:

45 × 9

So, 45 × 9 = 360 + 45

= 405

(b) 507 × 7

Solution:

507 × 7

So, 507 × 7

= 500 × 7 + 7 × 7

= 3549

(c) 94 ÷ 4

Solution:

When 94 is divided by 4, the quotient is 23 (i.e., 10 + 10 + 3), with a remainder of 2.

(d) 778 ÷ 6

Solution: 

When 778 is divided by 6, the quotient is 129 (i.e., 100 + 10 + 10 + 5 + 4), with a remainder of 4.

(e) 94 × 5

Solution:

94 × 5

So, 94 × 5

= 90 × 5 + 4 × 5

= 450 + 20

= 470 

(f) 396 × 4

Solution:

396 × 4
So, 396 × 4
= 300 × 4 + 90 × 4 + 6 × 4
= 1200 + 360 + 24
= 1584

(g) 83 ÷ 3

Solution:

When 83 is divided by 3, the quotient is 27 (i.e., 10 + 10 + 5 + 2), with a remainder of 2.

(h) 635 ÷ 5

Solution: 

When 635 is divided by 5, the quotient is 127 (i.e., 100 + 10 + 10 + 7).

Question 7. In mathematics, some statements are always true, some are sometimes true, and some are never true. Tick (√) in the appropriate column.

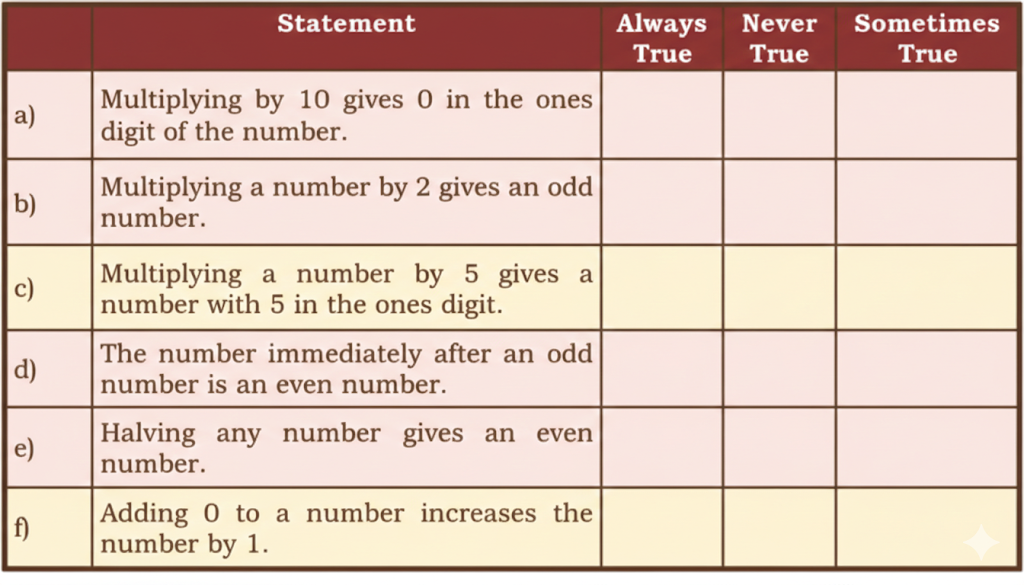
Solution:

Understanding Equal Groups and Multiplication

Class 4 students learn how equal groups connect to multiplication and division using fun stories like animal jumps and Gulabo’s garden. These NCERT Solutions Class 4 Maths Chapter 9 Equal Groups (2025-26) make every concept easy to visualise.

By practising problems on common multiples, doubling, and sharing equally, children build a strong base for higher classes. NCERT Solutions Class 4 Maths Chapter 9 Equal Groups help them see multiplication as repeated addition and division as equal sharing.

While revising NCERT Solutions Class 4 Maths Chapter 9 Equal Groups (2025-26), try drawing jumps on number lines or making your own word sums. Regular practice of these exercise-based questions boosts accuracy, speed, and confidence for school exams.