Class 7 Maths Chapter 1 NCERT Solutions: Large Numbers Around Us

1.1 A Lakh Varieties!

NCERT In-Text Questions (Pages 1-3)

Eshwarappa shared this incident with his daughter, Roxie, and son Estu. Estu was surprised to know that there were about one lakh varieties of rice in this country. He wondered, “One lakh! So far, I have only tasted 3 varieties. If we tried a new variety each day, would we even come close to tasting all the varieties in a lifetime of 100 years?” What do you think? Guess.

Solution:
One lakh is represented as 1,00,000 in figures.
If Roxie and Estu try a new variety every day, then they can taste 365 varieties in a year (since there are 365 days in a year).

To taste all 1,00,000 varieties, they would need 1,00,000 + 365 ~ 274 years.
Since 274 years is much longer than an average human lifetime, so Roxie and Estu would not be able to taste all the varieties in their lifetime- even if they tried a new one every single day!

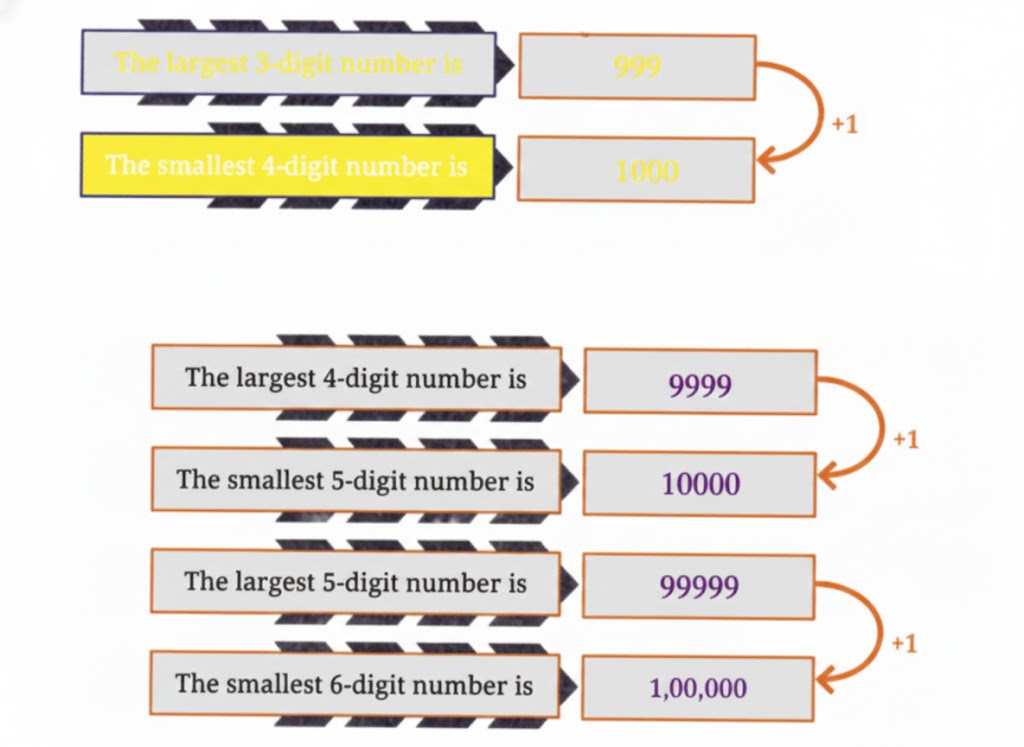
But how much is one lakh? Observe the pattern and fill in the boxes given below.

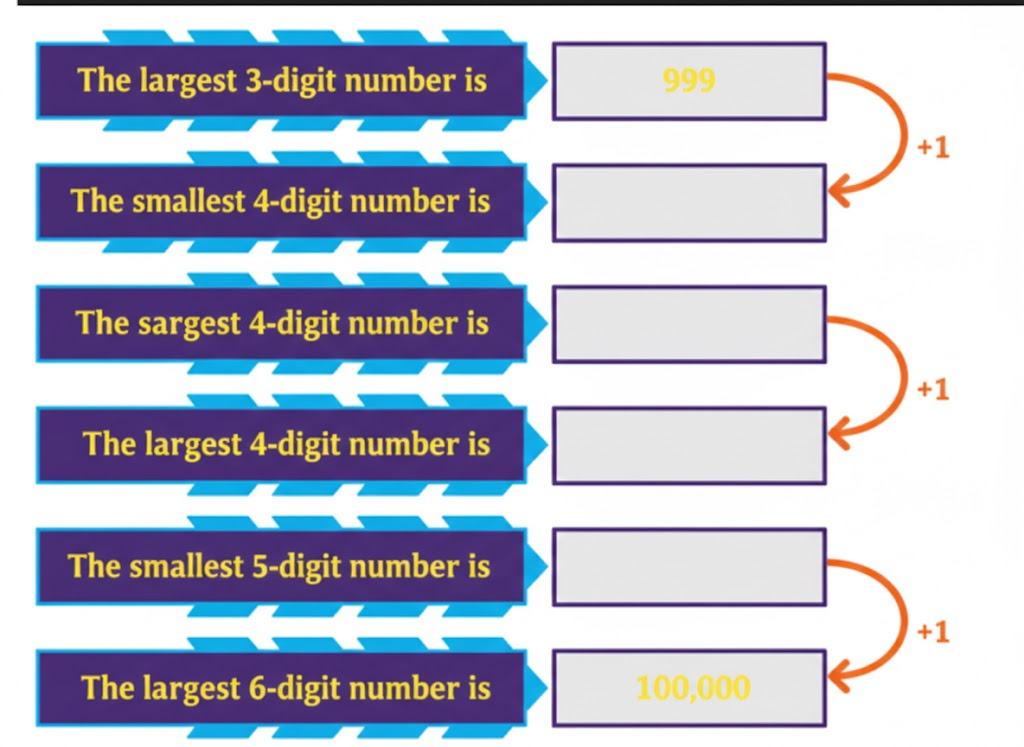
Solution:

Roxie and Estu …. 100 years?”

Solution:

If Roxie and Estu taste 2 varieties of rice each day, then in one year they can try:

365 × 2 = 730 varieties

To finish all 1,00,000 varieties, the number of years needed would be:

1,00,000 ÷ 730 ≈ 137 years

So, even at this rate, they cannot finish tasting all 1 lakh varieties of rice within 100 years.

What if a person ate 3 varieties of rice every day? Will they be able to taste all the lakh varieties in a 100-year lifetime? Find out.

Solution: If they taste 3 varieties of rice each day, then in one year they can try:

365 × 3 = 1,095 varieties

To finish all 1,00,000 varieties, they would need:

1,00,000 ÷ 1,095 ≈ 91 years

So, at this rate, they would be able to taste all 1 lakh varieties of rice within 100 years.

Choose a number for y. How close to one lakh is the number of days in y years, for the y of your choice?

Solution: To find the number of days in y years, we multiply:

365 × y

For 1,00,000 days, the number of years required is:

1,00,000 ÷ 365 ≈ 273 years

So, 1,00,000 days is approximately 273 years.

Thus, we have 365 × y = 365 × 273 ~ 99645 days (closest to 1 lakh)

Figure it Out (Page 3)

1. According to the 2011 Census, the population of the town of Chintamani was about 75,000. How much less than one lakh is 75,000?

Solution:

One lakh equals 1,00,000.

Now, 1,00,000 – 75,000 = 25,000.

Therefore, in 2011, the population of Chintamani was 25,000 less than one lakh.

2. The estimated population of Chintamani in the year 2024 is 1,06,000. How much more than one lakh is 1,06,000?

Solution: 1,06,000 – 1,00,000 = 6,000

So, the population in 2024 is 6,000 more than one lakh.

3. By how much did the population of Chintamani increase from 2011 to 2024?

Solution: The rise in population from 2011 to 2024 is:

1,06,000 – 75,000 = 31,000

So, the population increased by 31,000 people during this period.

Getting a Feel of Large Numbers

You may have come across interesting facts like these:

• The world’s tallest statue is the ‘Statue of Unity’ in Gujarat depicting Sardar Vallabhbhai Patel. Its height is about 180 metres.

• Kunchikal waterfall in Karnataka is said to drop from a height of about 450 metres.

It is not always easy to get a sense of how big these measurements are. But, we can get a better sense of their size when we compare them with something familiar. Let us see an example.

NCERT In-Text Questions (Page 3)

Look at the picture on the right. Somu is 1 metre tall. If each floor is about four times his height, what is the approximate height of the building?

Solution:

Somu’s height = 1 m

Height of a floor = 4 × Somu’s height

= 4 × 1 m

= 4 m

Approximate height of the building = Height of 11 floors

= 11 × 4 m

= 44 m

Which is taller — The Statue of Unity or this building? How much taller?

__________ m

Solution:

The Statue of Unity is 180 m tall, and the building is 44 m tall.

Difference in heights = 180 – 44 = 136 m.

The Statue of Unity is taller than the building.

How much taller is the Kunchikal waterfall than Somu’s building?

__________ m

Solution:

Kunchikal waterfall is 450 m tall, and the building is 40 m tall.

Difference in heights = 450 – 44 = 406 m

Thus, the Kunchikal waterfall is 406 m taller than the building.

How many floors should Somu’s building have to be as high as the waterfall?
__________

Solution:
Each floor is 4 m tall. To match the height of the waterfall (450 m), floors needed = 450 ÷ 4 = 112.5.
Thus, building would need approximately 113 floors to be as high as the waterfall.

Is One Lakh a Very Large Number?

NCERT In-Text Questions (Page 4)

How do you view a lakh — is a lakh big or small?

Solution: One lakh is considered a large number when we talk about counting.

Reading and Writing Numbers

NCERT In-Text Questions (Pages 4-5)

Write each of the numbers given below in words:
(a) 3,00,600
(b) 5,04,085
(c) 27,30,000
(d) 70,53,138

Solution:
(a) 3,00,600 → Three lakh six hundred
(b) 5,04,085 → Five lakh four thousand eighty-five
(c) 27,30,000 → Twenty-seven lakh thirty thousand
(d) 70,53,138 → Seventy lakh fifty-three thousand one hundred thirty-eight

Write the corresponding number in the Indian place value system for each of the following:
(a) One lakh twenty-three thousand four hundred fifty-six
(b) Four lakh seven thousand seven hundred four
(c) Fifty lakh five thousand fifty
(d) Ten lakh two hundred thirty-five

Solution:
(a) 1,23,456
(b) 4,07,704
(c) 50,05,050
(d) 10,00,235

1.2 Land of Tens

NCERT In-Text Questions (Pages 5-6)

1. The Thoughtful Thousands only has a + 1000 button. How many times should it be pressed to show:

(a) Three thousand? 3 times

(b) 10,000? ___________

(c) Fifty-three thousand? ___________

(d) 90,000? ___________

(e) One Lakh? ___________

(f) ___________? 153 times

(g) How many thousands are required to make one lakh?

Solution:

(b) 10 times

(c) 53 times

(d) 90 times

(e) 100 times

(f) 1,53,000

(g) 100 thousands

2. The Tedious Tens only has a +10 button. How many times should it be pressed to show:

(a) Five hundred?

(b) 780?

(c) 1000?

(d) 3700?

(e) 10,000?

(f) One lakh?

(g) __________? 435 times

Solution:

(a) 50 times

(b) 78 times

(c) 100 times

(d) 370 times

(e) 1000 times

(f) 10,000 times

(g) 4350

3. The Handy Hundreds only has a +100 button. How many times should it be pressed to show:

(a) Four hundred? __________ times
(b) 3,700? __________
(c) 10,000? __________
(d) Fifty-three thousand? __________
(e) 90,000? __________
(f) 97,600? __________
(g) 1,00,000? __________
(h) __________? 582 times
(i) How many hundreds are required to make ten thousand?
(j) How many hundreds are required to make one lakh?
(k) Handy Hundreds says, “There are some numbers which Tedious Tens and Thoughtful Thousands can’t show but I can.” Is this statement true? Think and explore.

Solution:
(a) 4 times
(b) 37 times
(c) 100 times
(d) 530 times
(e) 900 times
(f) 976 times
(g) 1000 times
(h) 58200
(i) 100 hundreds
(j) 1,000 hundreds
(k) Do it yourself.

4. Creative Chitti is a different kind of calculator. It has the following buttons:

+1, +10, +100, +1000, +10000, +100000, and +1000000.

It always has multiple ways of doing things. “How so?”, you might ask. To get the number 321, press +10 thirty-two times and +1 once. Will it get 321? Alternatively, it can press +100 two times and +10 twelve times, and +1 once.

Solution:
Yes.

5. Two of the many different ways to get 5072 are shown below:

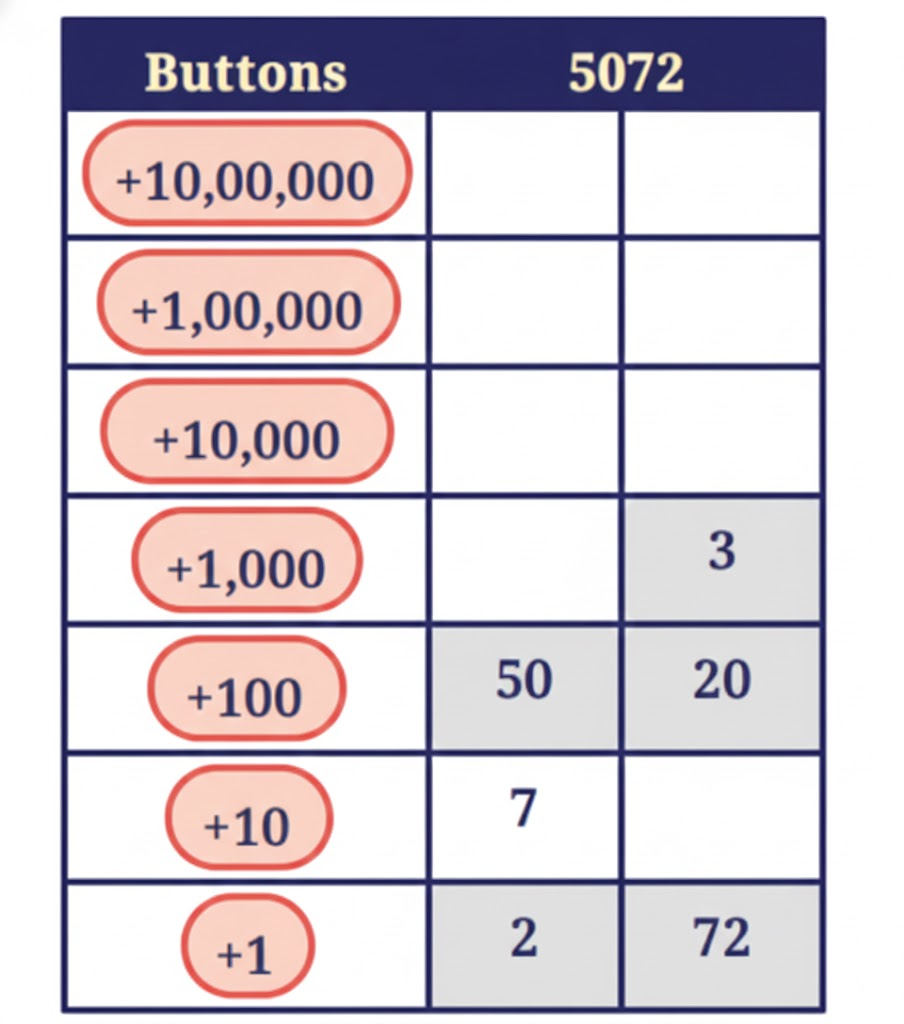
These two ways can be expressed as:

(a) (50 × 100) + (7 × 10) + (2 × 1) = 5072

(b) (3 × 1000) + (20 × 100) + (72 × 1) = 5072

Find a different way to get 5072 and write an expression for the same.

Solution:

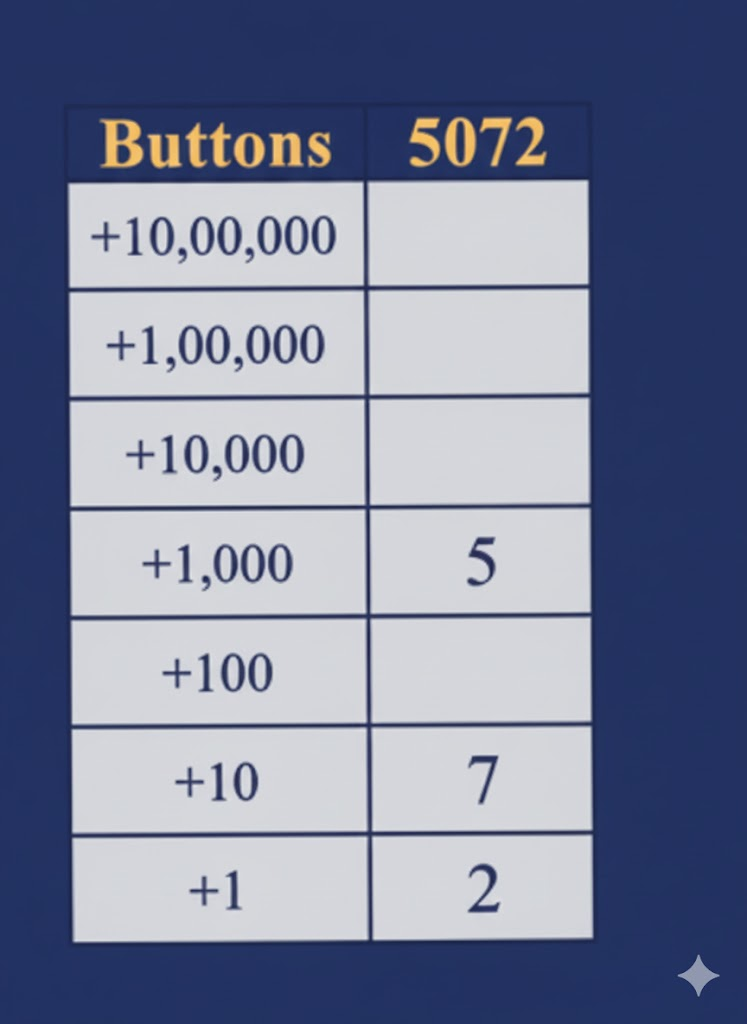
5 × 1000 + 7 × 10 + 2 × 1

Figure it Out (Pages 6-7)

For each number given below, write expressions for at least two different ways to obtain the number through button clicks. Think like Chitti and be creative.

(а) 8300
(b) 40629
(c) 56354
(d) 66666
(e) 367813

Solution:
(a) (i) (8 × 1000) + (3 × 100) = 8300
(ii) (83 × 100) = 8300

(b) (i) (4 × 10000) + (6 × 100) + (2 × 10) + (9 × 1) = 40629
(ii) (40 × 1000) + (6 × 100) + (29 × 1) = 40629

(c) (i) (5 × 10000) + (6 × 1000) + (3 × 100) + (54 × 1) = 56354
(ii) (56 × 1000) + (35 × 10) + (4 × 1) = 56354

(d) (i) (6 × 10000) + (6 × 1000) + (6 × 100) + (66 × 1) = 66666
(ii) (66 × 1000) + (66 × 10) + (6 × 1) = 66666

(e) (i) (3 × 100000) + (6 × 10000) + (7 × 1000) + (8 × 100)+ (13 × 1) = 367813
(ii) (36 × 10000) + (7813 × 1) = 367813

NCERT In-Text Questions (Page 7)

Creative Chitti has some questions for you-

(a) You have to make exactly 30 button presses. What is the largest 3-digit number you can make? What is the smallest 3-digit number you can make?
(b) 997 can be made using 25 clicks. Can you make 997 with a different number of clicks?

Solution:

(a) Largest and Smallest 3-Digit Numbers Using Limited Clicks

Largest 3-digit number:
To make the largest possible 3-digit number using a total of 30 clicks:

• Press +100 button 9 times → 9 × 100 = 900
  
  

• Press +10 button 8 times → 8 × 10 = 80
  
  

• Press +1 button 13 times → 13 × 1 = 13
  
  

Total: 900 + 80 + 13 = 993
So, the largest 3-digit number possible is 993.

Smallest 3-digit number:
To make the smallest possible 3-digit number using a total of 30 clicks:

• Press +10 button 8 times → 80
  
  

• Press +1 button 22 times → 22
  
  

Total: 80 + 22 = 102
So, the smallest 3-digit number possible is 102.

(b) Forming 997 Using 34 Clicks

• 9 × (+100) = 900
  
  

• 8 × (+10) = 80
  
  

• 17 × (+1) = 17
  
  

Total: 900 + 80 + 17 = 997

Create similar questions and challenge your classmates.

Solution:
Do it yourself.

Systematic Sippy is a different kind of calculator. It has the following buttons:

+1, +10, +100, +1000, +10000, +100000.
It wants to be used as minimally as possible.

How can we get the numbers (a) 5072, (b) 8300 using as few button clicks as possible?

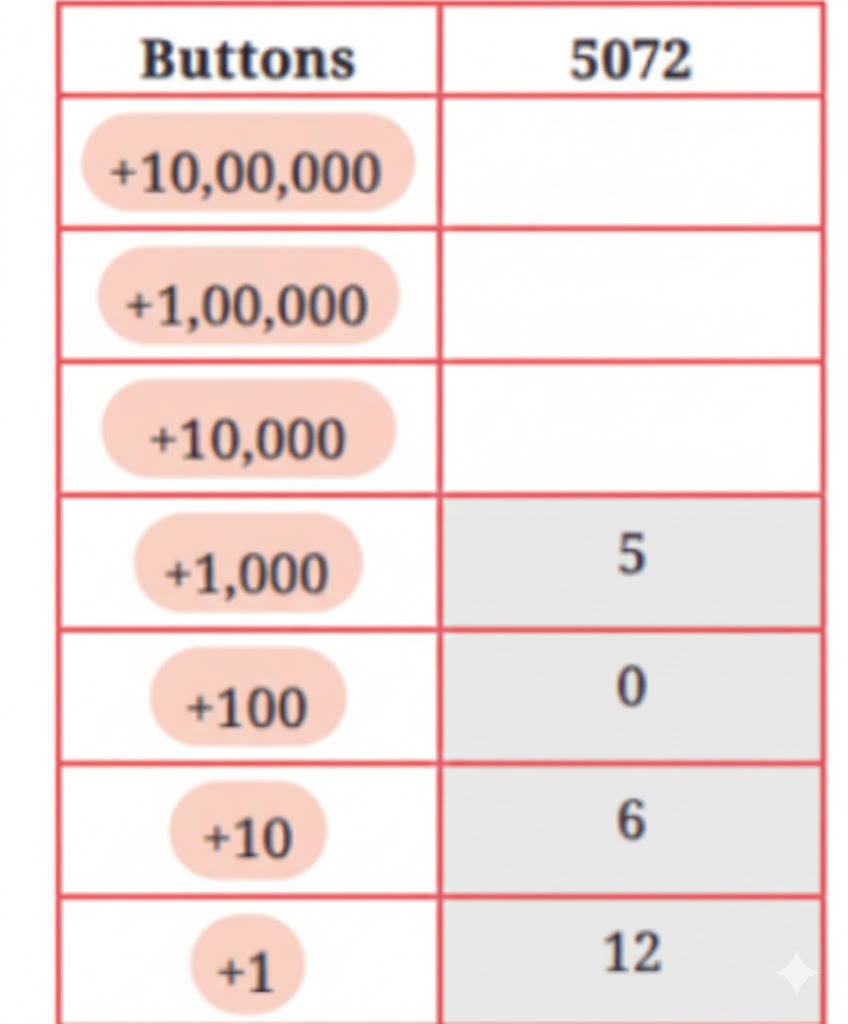
Find out which buttons should be clicked and how many times to get the desired numbers given in the table. The aim is to click as few buttons as possible.

Here is one way to get the number 5072. This method uses 23 button clicks in total.

Is there another way to get 5072 using fewer than 23 button clicks?

Write the expression for the same.

Solution:

(a) 5 × (+1000) = 5000 (5 clicks)

7 × (+10) = 70 (7 clicks)

2 × (+1) = 2 (2 clicks)

Total clicks: 5 + 7 + 2 = 14 clicks

Expression: 5 × 1000 + 7 × 10 + 2 × 1 = 5072

(b)

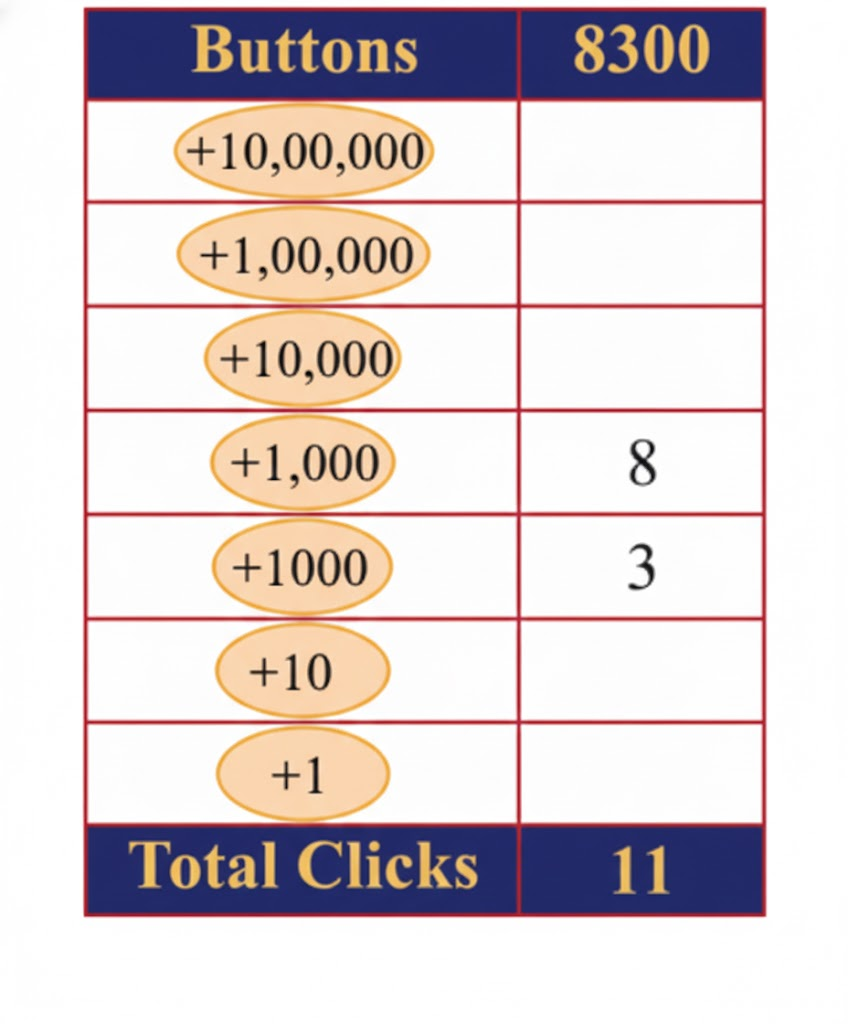
For 8300: 8 × (+1000) = 8000

For: 3 × (+100) = 300

Total = 8000 + 300 = 8300

Figure it Out (Page 7)

1. For the numbers in the previous exercise, find out how to get each number by making the smallest number of button clicks, and write the expression.

Solution:
(a) 8300
8 × (+1000) = 8000 (8 clicks)
3 × (+100) = 300 (3 clicks)
Total clicks: 8 + 3 = 11
Expression: (8 × 1000) + (3 × 100) = 8300

(b) 40629
4 × (+10000) = 40000 (4 clicks)
6 × (+100) = 600 (6 clicks)
2 × (+10) = 20 (2 clicks)
9 × (+1) = 9 (9 clicks)
Total clicks: 4 + 6 + 2 + 9 = 21
Expression: (4 × 10000) + (6 × 100) + (2 × 10) + (9 × 1) = 40629

(c) 56354
5 × (+10000) = 50000 (5 clicks)
6 × (+1000) = 6000 (6 clicks)
3 × (+100) = 300 (3 clicks)
5 × (+10) = 50 (5 clicks)
4 × (+1) = 4 (4 clicks)
Total clicks: 5 + 6 + 3 + 5 + 4 = 23
Expression: (5 × 10000) + (6 × 1000) + (3 × 100) + (5 × 10) + (4 × 1) = 56354

(d) 66666
6 × (+10000) = 60000 (6 clicks)
6 × (+1000) = 6000 (6 clicks)
6 × (+100) = 600 (6 clicks)
6 × (+10) = 60 (6 clicks)
6 × (+1) = 6 (6 clicks)
Total clicks: 6 + 6 + 6 + 6 + 6 = 30
Expression: (6 × 10000) + (6 × 1000) + (6 × 100) + (6 × 10) + (6 × 1) = 66666

(e) 367813
3 × (+100000) = 300000 (3 clicks)
6 × (+10000) = 60000 (6 clicks)
7 × (+1000) = 7000 (7 clicks)
8 × (+100) = 800 (8 clicks)
1 × (+10)= 10(1 click)
3 × (+1) = 3 (3 dicks)
Total clicks: 3 + 6 + 7 + 8 + 1 + 3 = 28
Expression: (3 × 100000) + (6 × 10000) + (7 × 1000) + (8 × 100) + (1 × 10) + (3 × 1) = 367813

2. Do you see any connection between each number and the corresponding smallest number of button clicks?

Solution: The minimum number of button clicks depends on the place value of each digit in the number. A smaller digit requires fewer clicks, while a larger digit requires more clicks to reach the desired value.

3. If you notice, the expressions for the least button clicks also give the Indian place value notation of the numbers. Think about why this is so.

Solution:
Do it yourself.

1.3 Of Crores and Crores!

NCERT In-Text Questions (Pages 8-9)

How many zeros does a thousand lakh have?

Solution:
1,000 lakh = 10,00,00,000 (8 zeros)

How many zeros does a hundred thousand have?

Solution:
100 thousand = 1,00,000 (5 zeros)

Figure it Out (Page 9)

1. Read the following numbers in Indian place value notation and write their number names in both the Indian and American systems:

(a) 4050678
(b) 48121620
(c) 20022002
(d) 246813579
(e) 345000543
(f) 1020304050

Solution:
(a) Indian System
40.50.678 → 40 lakh 50 thousand and 678
Forty lakh fifty thousand six hundred seventy-eight

American System
4.050.678 → 4 million 50 thousand and 678
Four million fifty thousand six hundred seventy-eight

(b) Indian System
4.81.21.620 → 4 crore 81 lakh 21 thousand and 620
Four crore eighty-one lakh twenty-one thousand six hundred twenty

American System
48,121,620 → 48 million 121 thousand and 620
Forty-eight million one hundred twenty-one thousand six hundred twenty

(c) Indian System
2,0, 22,002 → 2 crore 22 thousand 2
Two crore twenty-two thousand two

American System:
20,022,002 → 20 million 22 thousand 2
Twenty million twenty-two thousand two

(d) Indian System
24,68,13,579 → 24 crore 68 lakh 13 thousand 579
Twenty-four crore sixty-eight lakh thirteen thousand five hundred seventy-nine

American System
246.813.579 → 246 million 813 thousand 579
Two hundred forty-six million eight hundred thirteen thousand five hundred seventy-nine

(e) Indian System:
34,50,00,543 → 34 crore 50 lakh 543
Thirty-four crore fifty lakh five hundred forty-three

American System:
345,000,543 → 345 million 543
Three hundred forty-five million five hundred forty-three

(f) Indian System:
1,020,304,050 → 1 arab 2 crore 3 lakh 4 thousand 50
One arab two crore three lakh four thousand fifty

American System:
1,020,304,050 → 1 billion 20 million 304 thousand 50
One billion twenty million three hundred four thousand fifty

2. Write the following numbers in Indian place value notation:

(a) One crore one lakh one thousand ten
(b) One billion one million one thousand one
(c) Ten crore twenty lakh thirty thousand forty
(d) Nine billion eighty million seven hundred thousand six hundred

Solution:
(a) 1,01,01,010
(b) 1,001,001,001
(c) 10,20,30,040
(d) 9,080,700,600

3. Compare and write ‘>’, ‘<’ or ‘=’:
(a) 30 thousand __________ 3 lakh
(b) 500 lakh __________ 5 million
(c) 800 thousand __________ 8 million
(d) 640 crore __________ 60 billion

Solution:
(a) 30 thousand < 3 lakh
(b) 500 lakh > 5 million
(c) 800 thousand < 8 million
(d) 640 crore < 60 billion

1.4 Exact and Approximate Values

Nearest Neighbours

NCERT In-Text Questions (Pages 11-12)

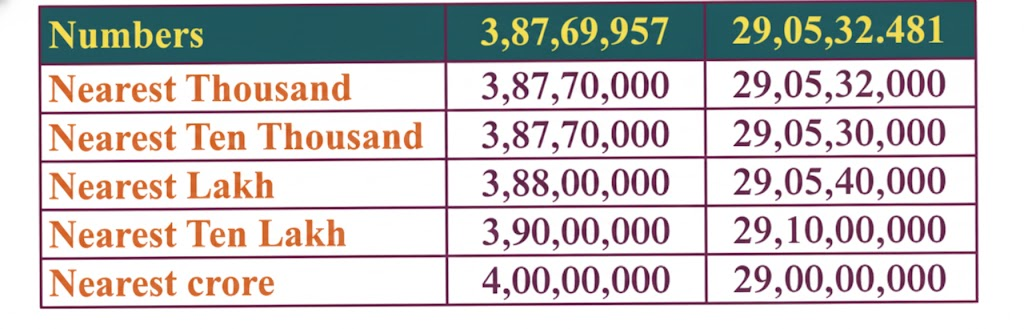
Write the five nearest neighbours for these numbers:

(a) 3,87,69,957

(b) 29,05,32,481

Solution:

I have a number for which all five nearest neighbours are 5,00,00,000. What could the number be? How many such numbers are there?

Solution:

4,99,99,999; Do it yourself.

Roxie and Estu are estimating the values of simple expressions.

1. 4,63,128 + 4,19,682

Roxie: “The sum is nearly 8,00,000 and is more than 8,00,000.”

Estu: “The sum is nearly 9,00,000 and is less than 9,00,000.”
(a) Are these estimates correct? Whose estimate is closer to the sum?
(b) Will the sum be greater than 8,50,000 or less than 8,50,000? Why do you think so?
(c) Will the sum be greater than 8,83,128 or less than 8,83,128? Why do you think so?
(d) Exact value of 4,63,128 + 4,19,682 = __________

Solution:
(a) By adding 4,63,128 and 4,19,682, we get 8,82,810 and the estimated sum is 5,00,000 + 4,00,000 = 9,00,000
The exact sum is 8,82,810, which is closer to 9,00,000.
Thus, Estu’s estimate is correct and closer to the actual sum.

(b) The exact sum is 8,82,810, which is clearly greater than 8,50,000.
If we estimate the two numbers (4,63,128 and 4,19,682) to the nearest ten thousands, we get 4,60,000 and 4,20,000.
By adding them, the results will be closer to 8,80,000, which is well above 8,50,000.

(c) The exact sum is 8,82,810, which is less than 8,83,128.
The sum falls short of 8,83,128 by only 318, making it closer to the actual sum.

(d) Exact value of 4,63,128 + 4,19,682 = 8,82,810

2. 14,63,128 – 4,90,020
Roxie: “The difference is nearly 10,00,000 and is less than 10,00,000.”
Estu: “The difference is nearly 9,00,000 and is more than 9,00,000”.
(a) Are these estimates correct? Whose estimate is closer to the difference?
(b) Will the difference be greater than 9,50,000 or less than 9,50,000? Why do you think so?
(c) Will the difference be greater than 9,63,128 or less than 9,63,128? Why do you think so?
(d) Exact value of 14,63,128 – 4,90,020 = ___________

Solution:
(a) The difference is: 14,63,128 – 4,90,020 = 9,73,108
The estimated difference = 15,00,000 – 5,00,000 = 10,00,000
But the numbers are rounded off to the highest value.
So, the difference should be less than 10,00,000.
Thus, Roxie’s estimate is closer to the actual difference.

(b) The exact difference is 9,73,108, which is clearly greater than 9,50,000.
If we estimate the numbers 14,63,128 and 4,90,020 to the nearest ten thousands place, we get 14,60,000 and 4,90,000 respectively.
By finding the difference, we get 9,70,000, which is more than 9,50,000.

(c) The exact difference is 9,73,108, which is greater than 9,63,128.
The difference exceeds 9,63,128 by 9,980, indicating it is far from the actual difference.

(d) Exact value of 14,63,128 – 4,90,020 = 9,73,108

Populations of the Cities

NCERT In-Text Questions (Page 13)

From the information given in the table, answer the following questions by approximation:

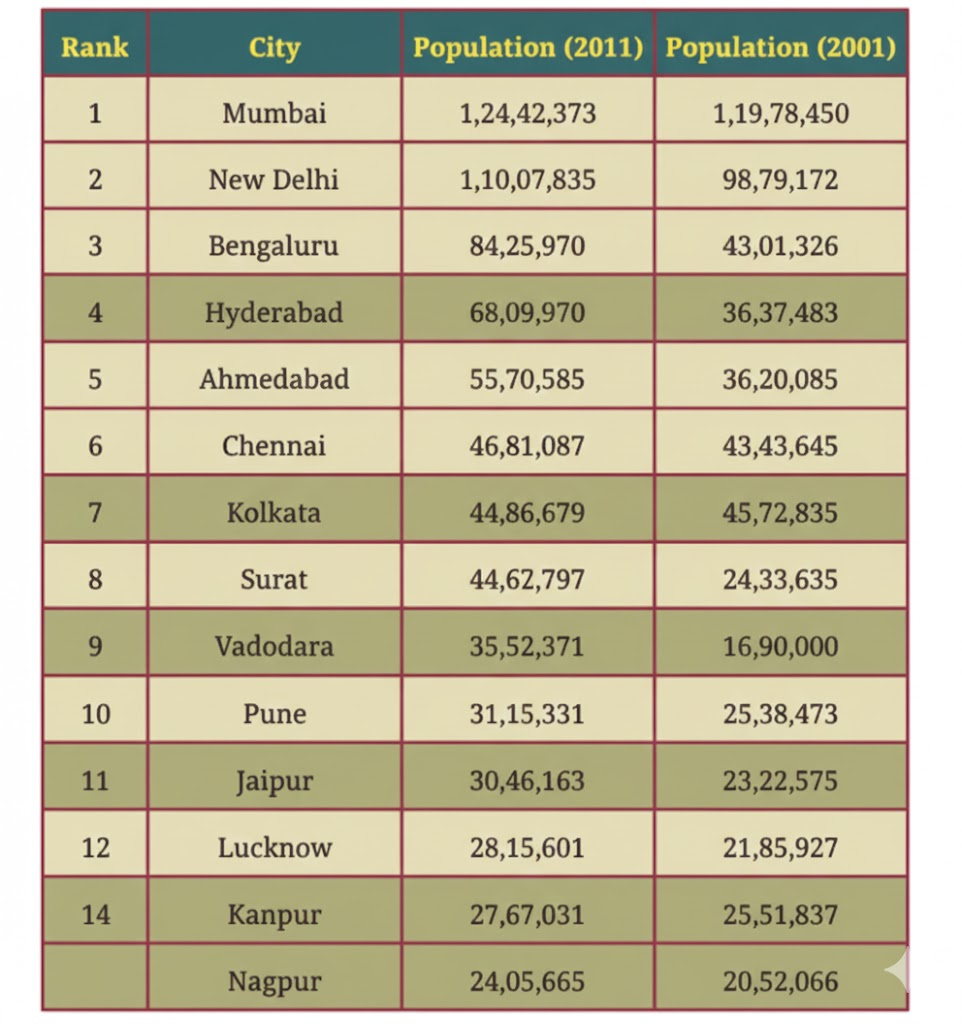
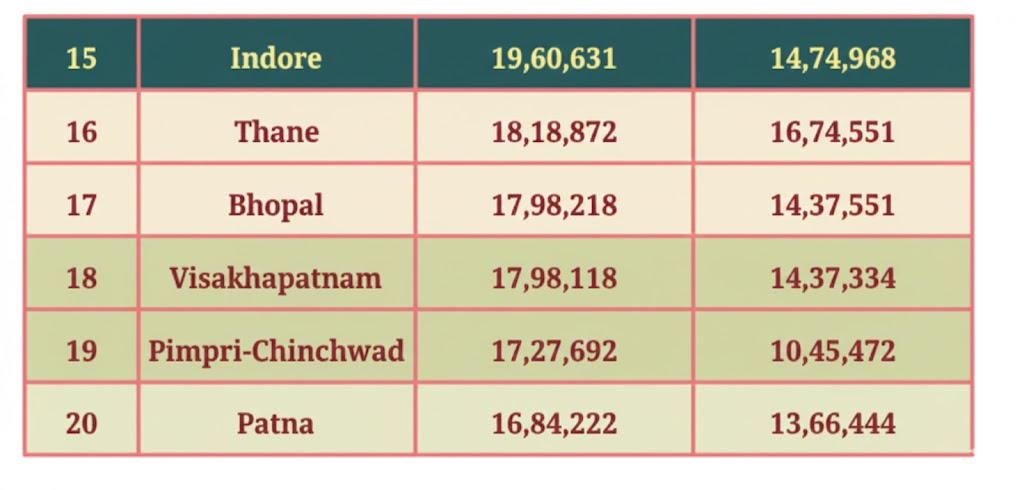
1. What is your general observation about this data? Share with the class.

Solution: The data presents the population of various Indian cities for the years 2001 and 2011.

2. What is an appropriate title for the above table?

Solution: Population of 20 major Indian cities in the years 2001 and 2011.

3. How much was the population of Pune in 2011? Approximately, by how much has it increased compared to 2001?

Solution: The population of Pune in 2011 was 31,15,431, and in 2001 it was 25,38,473.
The approximate increase in population is:

31,00,000 – 25,00,000 = 6,00,000

So, Pune’s population grew by about 6 lakh people.

4. Which city’s population increased the most between 2001 and 2011?

Solution:

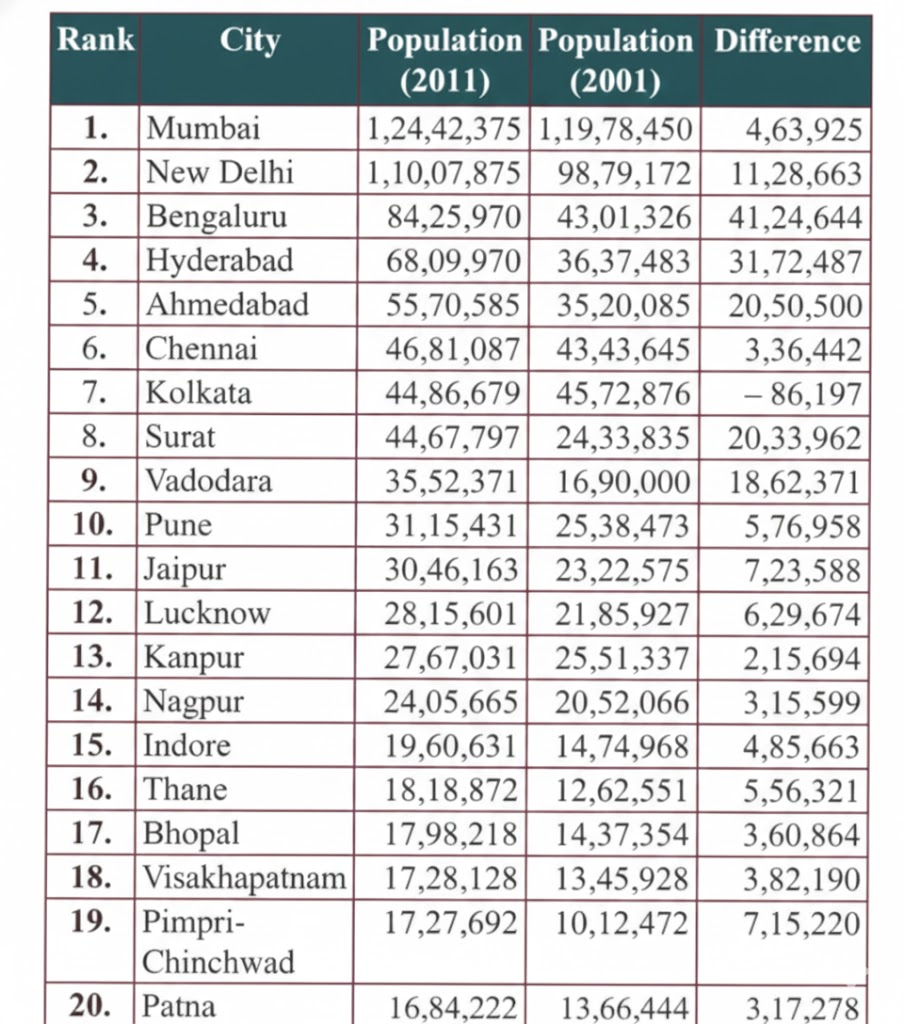
Bengaluru showed the highest rise in population, increasing by 41,24,644 people.

5. Are there cities whose population has almost doubled? Which are they?

Solution: Bengaluru, Hyderabad, Surat, Vadodara, and Pimpri-Chinchwad almost doubled their population between 2001 and 2011.

6. By what number should we multiply Patna’s population to get a number/population close to that of Mumbai?

Solution: Mumbai’s population divided by Patna’s population in 2011 is:

1,24,42,373 ÷ 16,84,222 ≈ 7

This means Patna’s population would need to be multiplied by about 7 to reach a number close to Mumbai’s population.

1.5 Patterns in Products

A Multiplication Shortcut

NCERT In-Text Questions (Page 14)

Using the meaning of multiplication and division, can you explain why multiplying by 5 is the same as dividing by 2 and multiplying by 10?

Solution:

We know that the multiplication fact 5 × 2 = 10 gives us two related division facts:
10 ÷ 2 = 5 and 10 ÷ 5 = 2.

So, based on the question, we can use 102 in place of 5.
Whether we divide 10 by 5 or by 102 (as required in the problem), we will get the corresponding division fact.

Figure it Out (Page 14)

1. Find quick ways to calculate these products:

(a) 2 × 1768 × 50
(b) 72 × 125 [Hint: 125 = 1000/8
(c) 125 × 40 × 8 × 25

Solution:

(a) 2 × 1768 × 50 = 2×1768×100/2

 = 1768 × 100

(b) 72 × 125 = 72×1000/8

 = 9 × 1000 = 9000

(c) 125 × 40 × 8 × 25 = 1000/8 ×40×8× 100/4

 = 10,00,000

2. Calculate these products quickly.

(a) 25 × 12 = __________

(b) 25 × 240 = __________

(c) 250 × 120 = __________

(d) 2500 × 12 = __________

(e) __________ × __________ = 120000000

Solution:

(a) 25 × 12 = 25 × 4 × 3 = 100 × 3 = 300

(b) 25 × 240 = 25 × 4 × 60 = 100 × 60 = 6000

(c) 250 × 120 = 250 × 4 × 30 = 1000 × 30 = 30000

(d) 2500 × 12 = 2500 × 4 × 3 = 10000 × 3 = 30000

(e) 25000 × 4800 = 120000000

How Long is the Product?

NCERT In-Text Questions (Pages 14-15)

In each of the following boxes, the multiplications produce interesting patterns. Evaluate them to find the pattern. Extend the multiplications based on the observed pattern.

Solution:

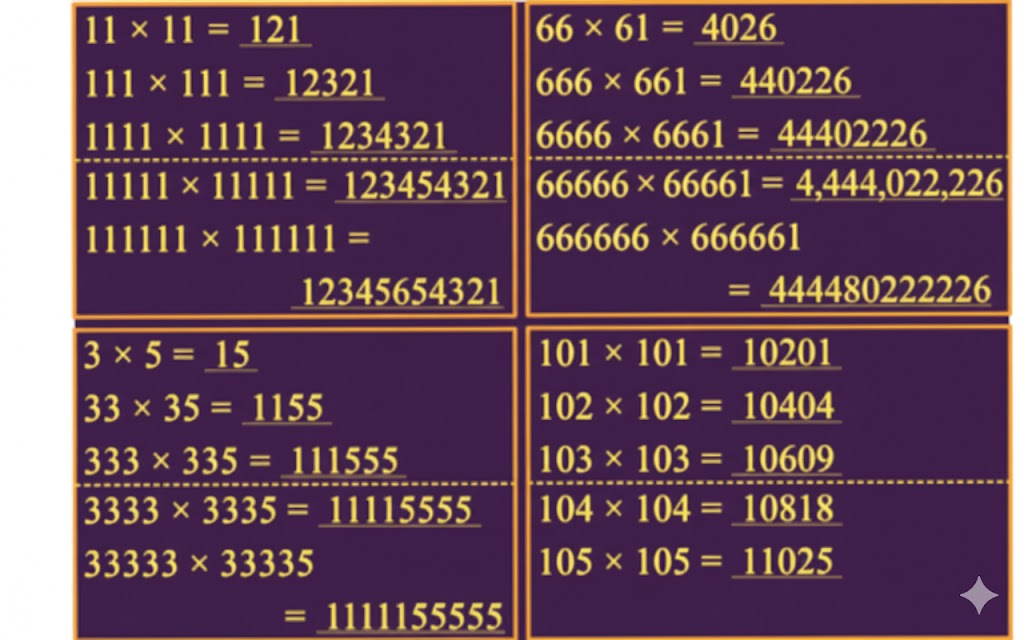
Observe the number of digits in the two numbers being multiplied and their product in each case. Is there any connection between the numbers being multiplied and the number of digits in their product?

Solution:
Yes, when we multiply:

• 1-digit number with a 1-digit number, we get a 1-digit or 2-digit product

• 2-digit number with a 2-digit number, we get a 3-digit or 4-digit product

• 3-digit number with a 3-digit number, we get a 5-digit or 6-digit product

• 4-digit number with a 4-digit number, we get a 7-digit or 8-digit product

Roxie says that the product of two 2-digit numbers can only be a 3- or a 4-digit number. Is she correct?

Solution:

Yes, Roxie is right because, based on the observed pattern, a 2-digit number multiplied by another 2-digit number results in either a 3-digit or a 4-digit product.

Should we try all possible multiplications with 2-digit numbers to tell whether Roxie’s claim is true? Or is there a better way to find out?

Solution: There is no need to try all possible multiplications to verify Roxie’s claim.
A better way is given in the examples below.
10 × 10 = 100 (3-digit), 10 being the smallest 2-digit number
99 × 99 = 9801 (4-digit), 99 being the largest 2-digit number

Can multiplying a 3-digit number by another 3-digit number give a 4-digit number?

Solution:

No, because multiplying a 3-digit number by another 3-digit number produces either a 5-digit or a 6-digit product.

Can multiplying a 4-digit number by a 2-digit number give a 5-digit number?

Solution:
Yes, as a 4-digit number × 2-digit number will give a 5-digit or 6-digit product.
1000 × 10 = 10000 (5-digit), 1000 and 10 being the smallest 4- and 2-digit numbers, respectively.
9999 × 99 = 989901 (6-digit), 9999 and 99 being the largest 4- and 2-digit numbers.

Observe the multiplication statements below. Do you notice any patterns? See if this pattern extends to other numbers as well.

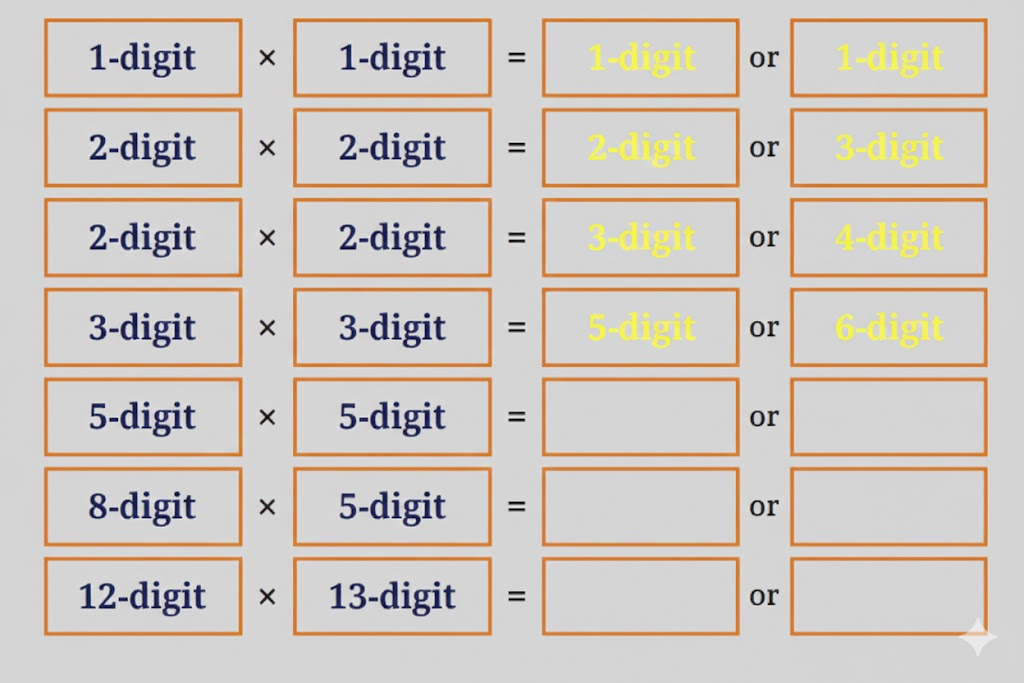
Solution:
Do it yourself.

1.6 Did You Ever Wonder…?

NCERT In-Text Questions (Page 19)

The RMS Titanic carried about 2500 passengers. Can the population of Mumbai fit into 5000 such ships?

Solution:

Total population of Mumbai = 1,24,00,000
Capacity of 5000 ships = 5000 × 2500 = 1,25,00,000

Yes, Mumbai’s population can easily fit into 5000 ships because their total capacity is greater than the city’s population.

Inspired by this unusual question, Roxie began to think:
“If I travel 100 kilometres every day, can I reach the Moon in 10 years?”
(The distance from the Earth to the Moon is 3,84,400 km.)

How far would she have travelled in a year?

Solution: Roxie travels in one year:

100 km per day × 365 days = 36,500 km

How far would she have travelled in 10 years?

Solution: Distance travelled by Roxie in 10 years = 100 km/day × 365 days × 10

= 36500 km × 10

= 365000 km

Is it not easier to perform these calculations in stages? You can use this method for all large calculations.

Solution:

Yes, breaking the calculations into smaller steps makes the process easier and more manageable.

Find out if you can reach the Sun in a lifetime, if you travel 1000 kilometres every day.

(You had written down the distance between the Earth and the Sun in a previous exercise)

Solution:

Distance between the Earth and the Sun = 2100 × 70,000 = 147000000 km

Distance travelled by you = 1000 km/day

Time required = 147000000 km ÷ 1000 km/day

= 147000 days

= 147000 days ÷ 365 days/year

~ 403 years

Not possible, as an average human being has a life expectancy of less than 100 years.

Make necessary reasonable assumptions and answer the questions below:
(a) If a single sheet of paper weighs 5 grams, could you lift one lakh sheets of paper together at the same time?
(b) If 250 babies are bom every minute across the world, will a million babies be bom in a day?
(c) Can you count 1 million coins in a day? Assume you can count 1 coin every second.

Solution:
(a) Weight of a single sheet = 5 grams.
Weight of 1 lakh sheets = 1,00,000 × 5 = 5,00,000 g = 500 kg, which is too heavy for any person to lift at once, as it exceeds normal human lifting capacity.
Thus, we couldn’t lift 1 lakh sheets together.

(b) Number of babies born every minute = 250
Total babies born in a day = 250 × 1440 = 3,60,000 babies
[Number of minutes in a day = 1440 minutes]
Thus, a million babies (1,000,000) will not be bom in a single day, as the daily count is 3,60,000 babies.

(c) Time taken to count 1 coin = 1 second.
In a single day, we can count 86,400 coins.
[Total seconds in a day = 24 × 60 × 60 = 86,400 seconds]
Thus, we cannot count 1 million coins in a day at the rate of 1 coin per second, since it would take approximately 1,000,000 ÷ 86,400 ~ 12 days to complete the task.

Figure it Out (Pages 19-21)

1. Using all digits from 0-9 exactly once (the first cannot be 0) to create a 10-digit number, write the

(a) Largest multiple of 5

(b) Smallest even number

Solution:

(a) To create the largest multiple of 5, the number must end in 0 or 5.
By arranging the digits in descending order and ending with 0 (the larger option for forming the maximum number), the largest possible multiple of 5 is:

9876543210 (a 10-digit number).

(b) To form the smallest even number, the last digit must be an even digit (0, 2, 4, 6, or 8).
We arrange the remaining digits in ascending order, making sure the number starts with the smallest non-zero digit.

Thus, the smallest 10-digit even number formed from all digits 0–9 is:

1023456789

(Here, 0 cannot be placed at the beginning, so it is moved to the second position.)

2. The number 10,30,285 in words is Ten lakhs thirty thousand two hundred eight five, which has 43 letters. Give a 7-digit number that has the maximum number of letters.

Solution: 77,77,777 (Seventy-seven lakh seventy-seven thousand seven hundred seventy-seven)
This number contains 61 letters, making it one of the longest 7-digit numbers when written in words.

3. Write a 9-digit number where exchanging any two digits results in a bigger number. How many such numbers exist?

Solution: For the number to increase in value no matter which two digits are swapped, its digits must already be in strictly increasing order from left to right. Therefore, the only arrangement that satisfies this rule is:

123456789

Thus, there is only one such number.

4. Strike out 10 digits from the number 12345123451234512345 so that the remaining number is as large as possible.

Solution: The number given is 12345123451234512345.
After removing the first 10 smallest digits from the left, the remaining number is:

5534512345

5. The words ‘zero’ and ‘one’ share letters ‘e’ and ‘o’. The words ‘one’ and ‘two’ share a letter ‘o’, and the words ‘two’ and ‘three’ also share a letter 7’. How far do you have to count to find two consecutive numbers that do not share an English letter in common?

Solution: The question asks for two consecutive numbers whose English names have no letters in common.

 However:

• zero and one share “e” and “o”
  
  

• one and two share “o”
  
  

• two and three share “t”
  
  

• …
  
  

• nineteen and twenty share “t”, “e”, and “n”
  
  

Continuing this pattern, every pair of consecutive numbers shares at least one letter. Therefore, no consecutive numbers exist whose English names have completely unique letters.

6. Suppose you write down all the numbers 1, 2, 3, 4,……., 9, 10, 11,….. The tenth digit you write is ‘1’ and the eleventh digit is ‘0’, as part of the number 10.

(a) What would the 1000th digit be? At which number would it occur?

(b) What number would contain the millionth digit?

(c) When would you have written the digit ‘5’ for the 5000th time?

Solution:

Numbers 1-9 contribute 9 digits (1 digit each).

Numbers 10-99 contribute 90 × 2 = 180 digits (2 digits each).

Numbers 100-999 contribute 900 × 3 = 2700 digits (3 digits each).

(a) To find the 1000th digit:
Digits so far: 9 + 180 = 189.
So, the 1000th digit will lie in the 3-digit numbers range.
Remaining digits: 1000 – 189 = 811.
Number of 3-digit numbers to reach 811 digits:
811 ÷ 3 = 270, with 1 remaining number.
Thus, first we need to write the first 270 3-digit numbers starting from 100.
So, the 270th 3-digit number = 100 + 270 – 1 = 369.
The next number is 370.
Thus, the 1000th digit is the 1st digit of 370, which is 3.

(b) Using the same logic:
Numbers 1-9: 9 digits
Numbers 10-99: 180 digits
Numbers 100-999: 2700 digits
Numbers 1000-9999: 9000 × 4 = 36,000 digits
Numbers 10,000-99,999: 90,000 × 5 = 4,50,000 digits
Numbers 1,00,000-9,99,999: 9,00,000 × 6 = 54,00,000 digits

To reach the millionth digit:
Upto 5-digit numbers: 9 + 180 + 2700 + 36,000 + 4,50,000 = 4,88,889
Remaining digits in the 6-digit range: 1,000,000 (or (10,00,000) – 4,88,889 = 5,11,111
The number of 6-digit numbers required: 5,11,111 ÷ 6 = 85,185, with 1 remaining number.
So, the 85,185th 6-digit number is 85,185 + 1,00,000 – 1 = 1,85,184.
The millionth digit occurs in the number 185184 + 1 = 1,85,185.

(c) Single-digit numbers (1-9): 1 (only 5)
Two-digit numbers (10-99)

• (15, 25, 35,…, 95), totaling 9 occurrences.

• 50, 51, 52, …, 59, totaling 10 occurrences.

Thus, 19 occurrences of the digit 5 in the range 10-99.
Total occurrences so far: 1 + 19 = 20

Three-digit numbers (100-999)

(i) Units position: Numbers like 105, 115, ….., 995 contribute 10 occurrences per 100 numbers. Across 900 numbers, there are 90 occurrences.

(ii) Tens position: Numbers like 150-159, 250-259, ……, 950-959 also contribute 10 occurrences per 100 numbers, and 90 occurrences in all.

(iii) Hundreds position: Numbers like 500-599 contribute 100 occurrences in this range.
Thus, 90 (units) + 90 (tens) + 100 (hundreds) = 280 occurrences
Total occurrences so far: 20 + 280 = 300

Four-digit numbers (1000-9999)
Now it gets more intense! Here, 5 appears in four positions (units, tens, hundreds, thousands):
(i) Units position: Every 10 numbers, e.g., 1005, 1015, …, 9995 = 900 occurrences total.

(ii) Tens position: 1050-1059, 1150-1159, …, 9950-9959. That’s 900 occurrences total.

(iii) Hundreds position: 1500-1599,2500-2599,…, 9500-9599 = 900 occurrences total.

(iv) Thousands position: 5000-5999 = 1000 occurrences
Adding these up: 900 (units) + 900 (tens) + 900 (hundreds) + 1000 (thousands) = 3700 occurrences

(v) Among 10000-10999, one digit 5 appears in 100 numbers (e.g., 10005, 10015,….., 10995).
The digit 5 appears in 100 numbers (e.g., 10050-10059, …, 10950-10959).
The digit 5 appears in 100 numbers (e.g., 10500-10599).
Total 4000 + 300 = 4300
In 11000-11999
5 at unit place = 100
5 at tens place = 100
5 at a hundred place = 100
Total 4300 + 300 = 4600
In 12000-12999
4600 + 300 = 4900
In 13000- 13999
Unit = 100
Total = 5000
Final number = 13995

7. A calculator has only ‘+10,000’ and ‘+100’ buttons. Write an expression describing the number of button clicks to be made for the following numbers:
(a) 20,800
(b) 92,100
(c) 1,20,500
(d) 65,30,000
(e) 70,25,700

Solution:
(a) 20,800 = 2 × 10,000 + 8 × 100
Number of clicks = 2 + 8 = 10 clicks

(b) 92,100 = 9 × 10,000 + 21 × 100

Number of clicks = 9 + 21 = 30 clicks

(c) 1,20,500 = 12 × 10,000 + 5 × 100
Number of clicks = 12 + 5 = 17 clicks

(d) 65,30,000 = 653 × 10,000 + 0 × 100
Number of clicks = 653 + 0 = 653 clicks

(e) 70,25,700 = 702 × 10,000 + 57 × 100
Number of clicks = 702 + 57 = 759 clicks

8. How many lakhs make a billion?

Solution:
1 lakh = 1,00,000
1 billion = 1,000,000,000
So, 1,000,000,000 ÷ 1,00,000 = 10,000.
Thus, 10,000 lakhs make a billion.

9. You are given two sets of number cards numbered from 1-9. Place a number card in each box below to get the (a) largest possible sum, (b) smallest possible difference of the two resulting numbers.

Solution:

(a) Largest possible sum = 9988776 + 65544 = 10054320

(b) Smallest possible difference = 1122334 – 99887 = 1022447

10. You are given some number cards: 4000, 13000, 300, 70000, 150000, 20, and 5. Using the cards, get as close as you can to the numbers below using any operation you want. Each card can be used only once to make a particular number.

(a) 1,10,000: Closest I could make is 4000 × (20 + 5) + 13000 = 1,13,000

(b) 2,00,000:

(c) 5,80,000:

(d) 12,45,000:

(e) 20,90,800:

Solution:

(a) 4000 × (20 + 5) + 13000

= 4000 × 25 + 13000

= 100000+ 13000

= 113000

This gives us 1,13,000, which is very close to 1,10,000.

(b) 1,50,000 + 70,000 – 4000 × 5 = 2,00,000

(c) 70,000 × 5 + 1,50,000 + 4,000 × 20 = 5,80,000

(d) 70,000 × 20 – 1,50,000 – 4,000 – 300 × 5 = 12,44,500
This gives us 12,44,500, which is very close to 12,45,000.

(e) 13,000 × 300 – 70,000(20 + 5) – 1,50,000 + 4,000 = 20,04,000

11. Find out how many coins should be stacked to match the height of the Statue of Unity. Assume each coin is 1 mm thick.

Solution:

The approximate height of the Statue of Unity is 180 metres, which is equal to 1,80,000 millimetres.
Given that the thickness of one coin is 1 mm,

To reach the same height, we would need:

1,80,000 coins

12. Grey-headed albatrosses have a roughly 7-foot wingspan. They are known to migrate across several oceans. Albatrosses can cover about 900-1000 km in a day. One of the longest single trips recorded is about 12,000 km. How many days would such a trip take to cross the Pacific Ocean approximately?

Solution: If the journey is done at 900 km per day:
12,000 ÷ 900 ≈ 13 days
So, it would take around 13 days.

If the journey is done at 1,000 km per day:
12,000 ÷ 1,000 = 12 days
So, it would take around 12 days.

Therefore, the 12,000 km trip would take approximately 12–13 days.

13. A bar-tailed godwit holds the record for the longest recorded non-stop flight. It travelled 13,560 km from Alaska to Australia without stopping. Its journey started on 13 October 2022 and continued for about 11 days. Find out the approximate distance it covered every day. Find out the approximate distance it covered every hour.

Solution: The total distance travelled is 13,560 km, and the journey takes 11 days.
So, the distance covered each day is:

13,560 ÷ 11 ≈ 1,233 km per day

Thus, the godwit flies about 1,233 km every day.

Since one day has 24 hours, the distance covered per hour is:

1,233 ÷ 24 ≈ 51 km per hour

Therefore, the godwit travels approximately 51 km per hour.

14. Bald eagles are known to fly as high as 4500 – 6000 m above the ground level. Mount Everest is about 8850 m high. Aeroplanes can fly as high as 10,000 – 12,800 m. How many times bigger are these heights compared to Somu’s building?

Solution: Bald eagle: 4,500–6,000 m

Ratios:

• 4,500 ÷ 44 ≈ 100
  
  

• 6,000 ÷ 44 ≈ 150
  
  

A bald eagle flies 100 to 150 times higher than Somu’s building.

Mount Everest: 8,850 m

Ratio:

• 8,850 ÷ 44 = 201
  
  

Mount Everest is 201 times taller than Somu’s building.

Aeroplanes: 10,000–12,800 m

Ratios:

• 10,000 ÷ 44 ≈ 230
  
  

• 12,800 ÷ 44 ≈ 290
  
  

An airplane flies 230 to 290 times higher than Somu’s building.

Learning About Large Numbers Around Us

The chapter on Large Numbers Around Us is essential for building a strong foundation in maths. By understanding lakhs, crores, and their place values, students can confidently solve numerical problems common in board exams.

Practising NCERT Solutions for Class 7 Maths Chapter 1 regularly helps students grasp place value, estimation, and the difference between the Indian and International systems. Pay attention to reading and writing numbers using commas for clarity.

To excel in exams, revise key concepts about large numbers and their patterns. Use visual aids and regular practice to boost your accuracy and speed, ensuring a high score in Maths in the NCERT 2025-26 syllabus.