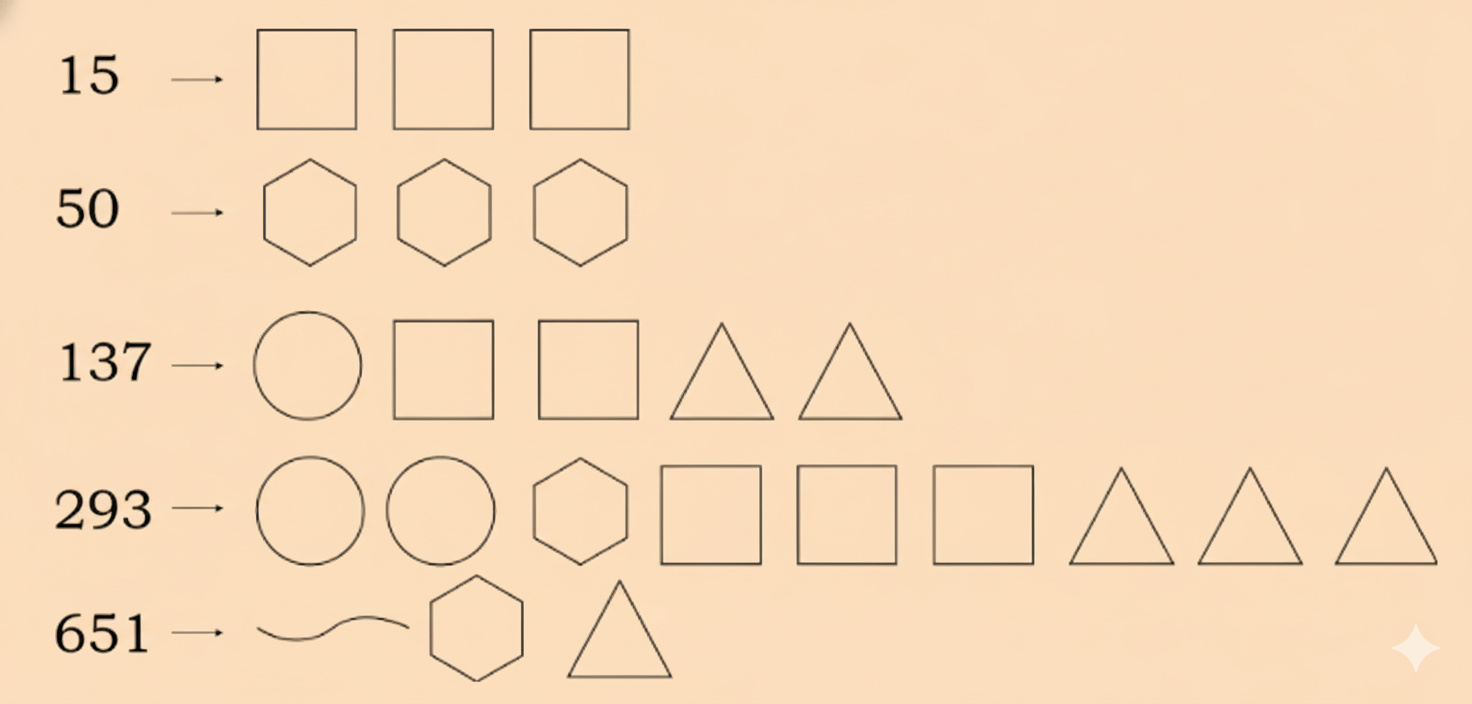
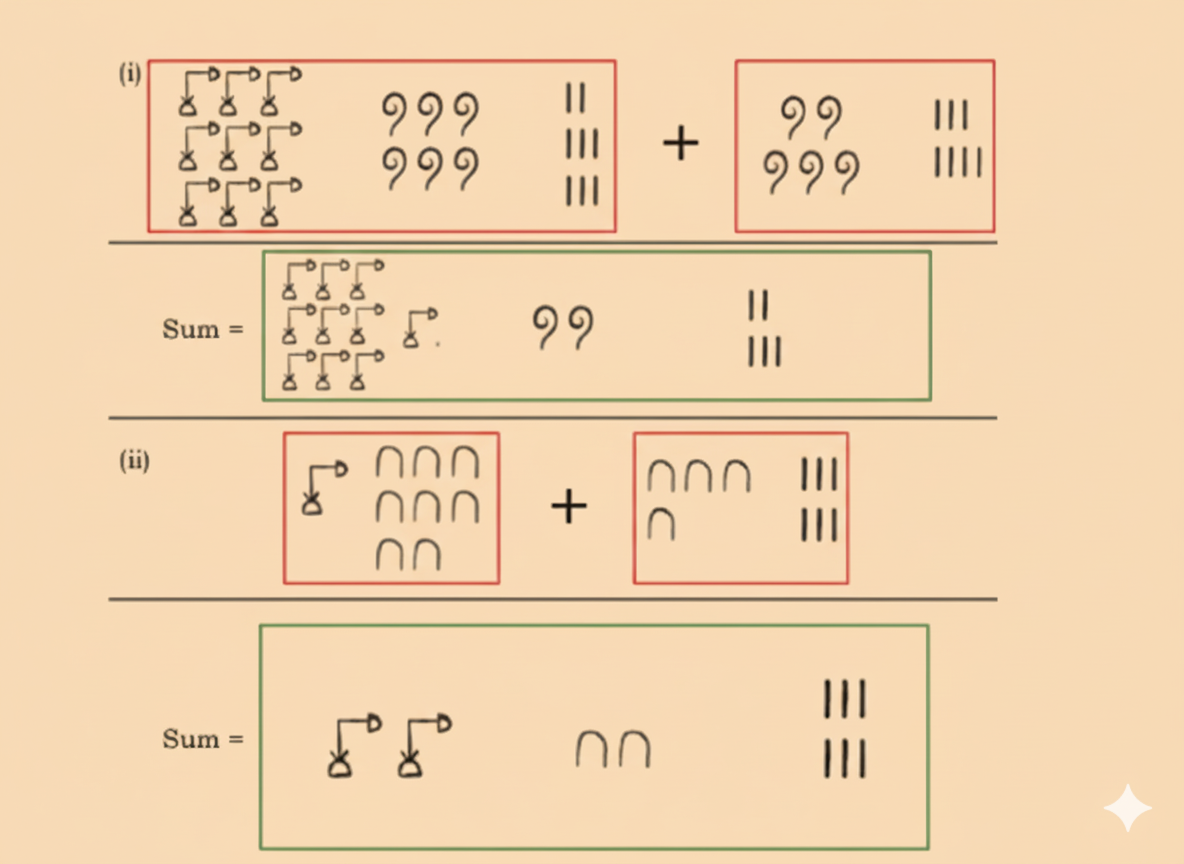
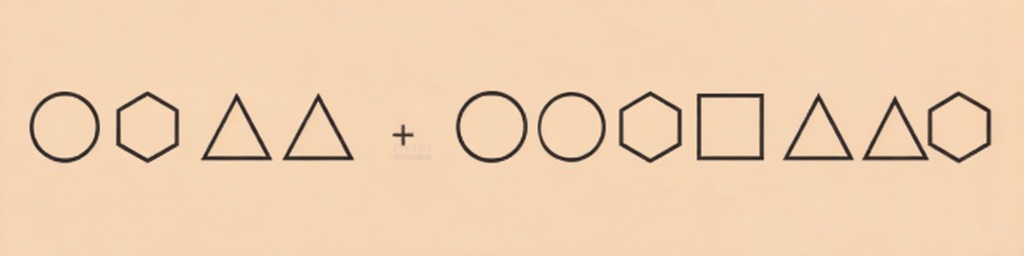
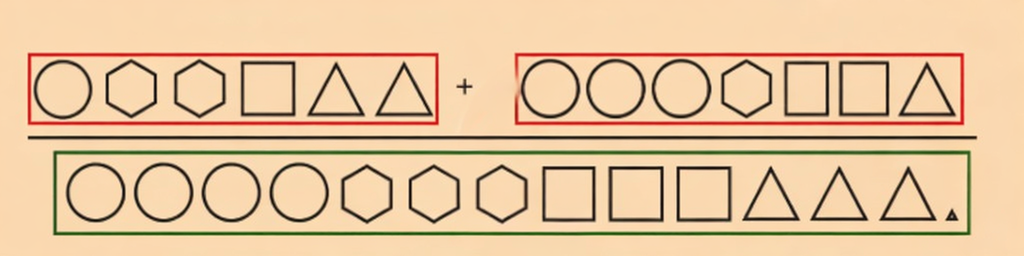
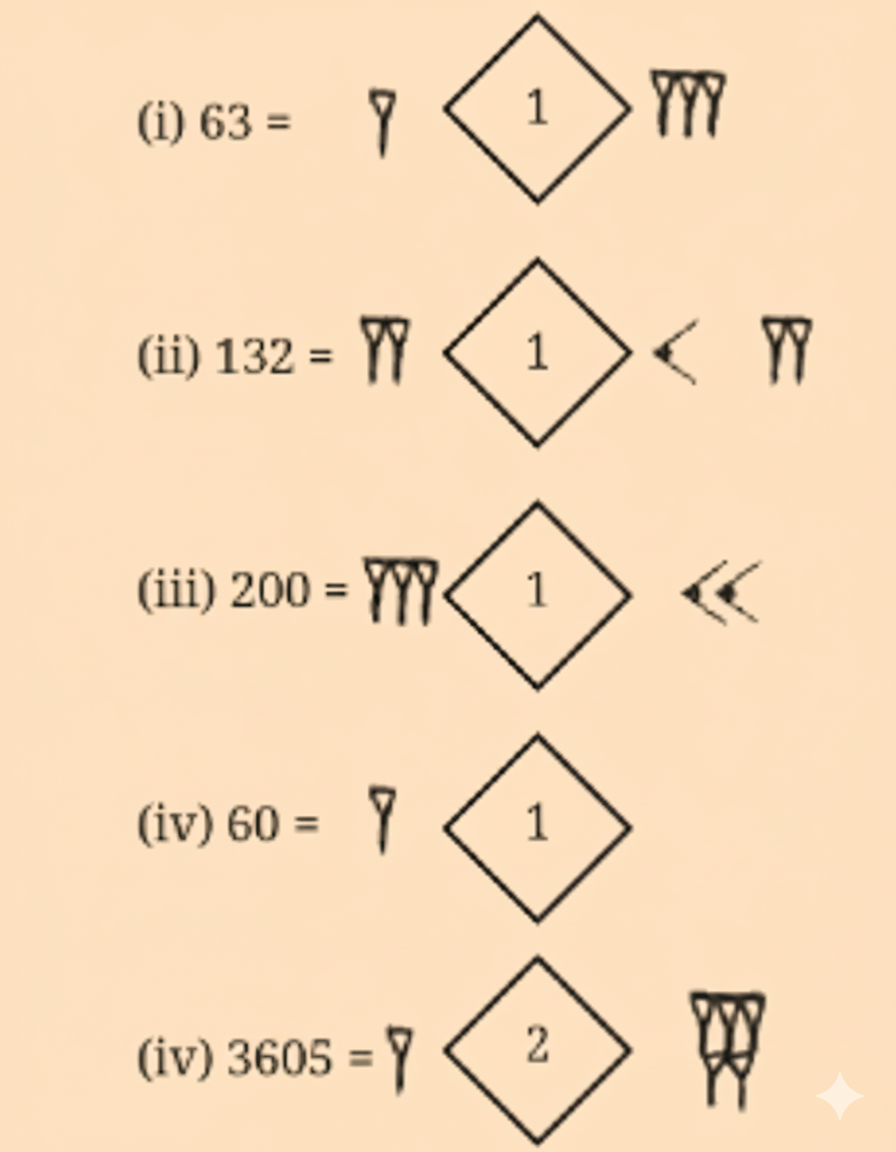
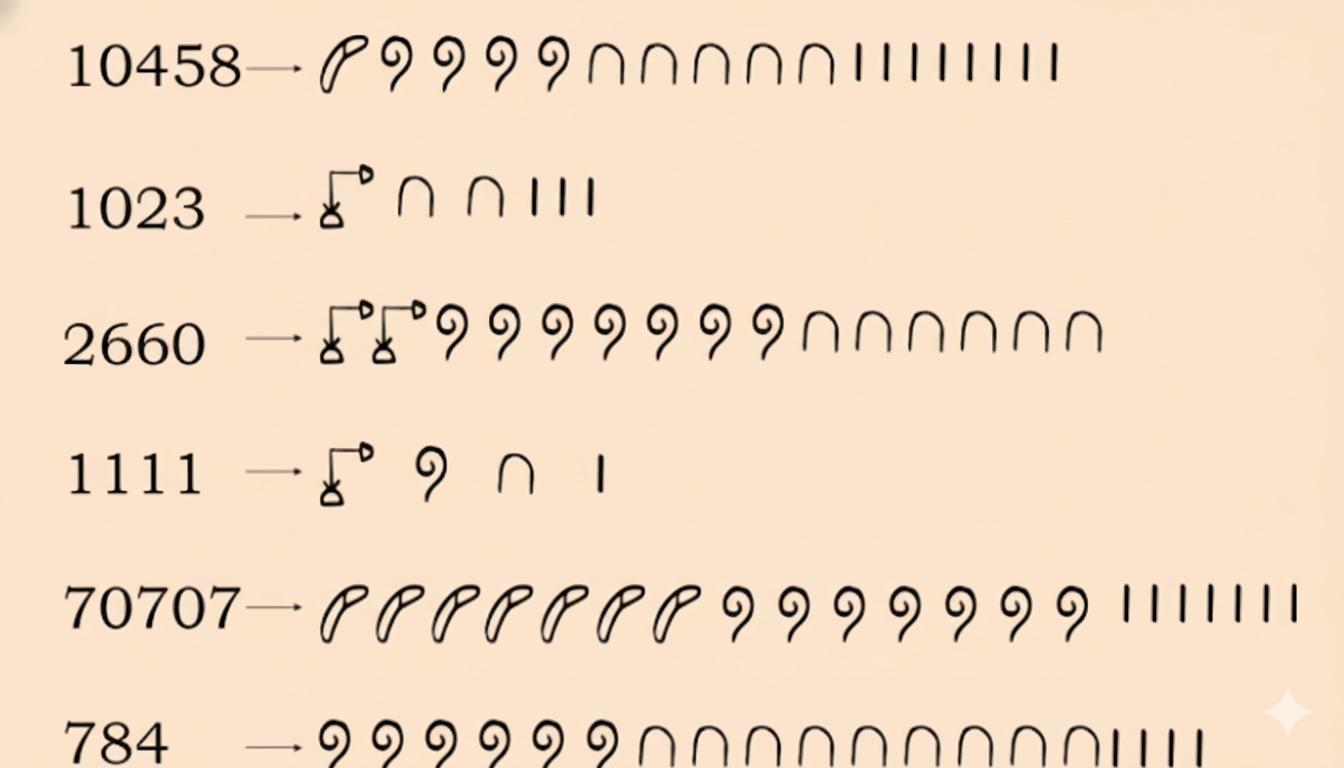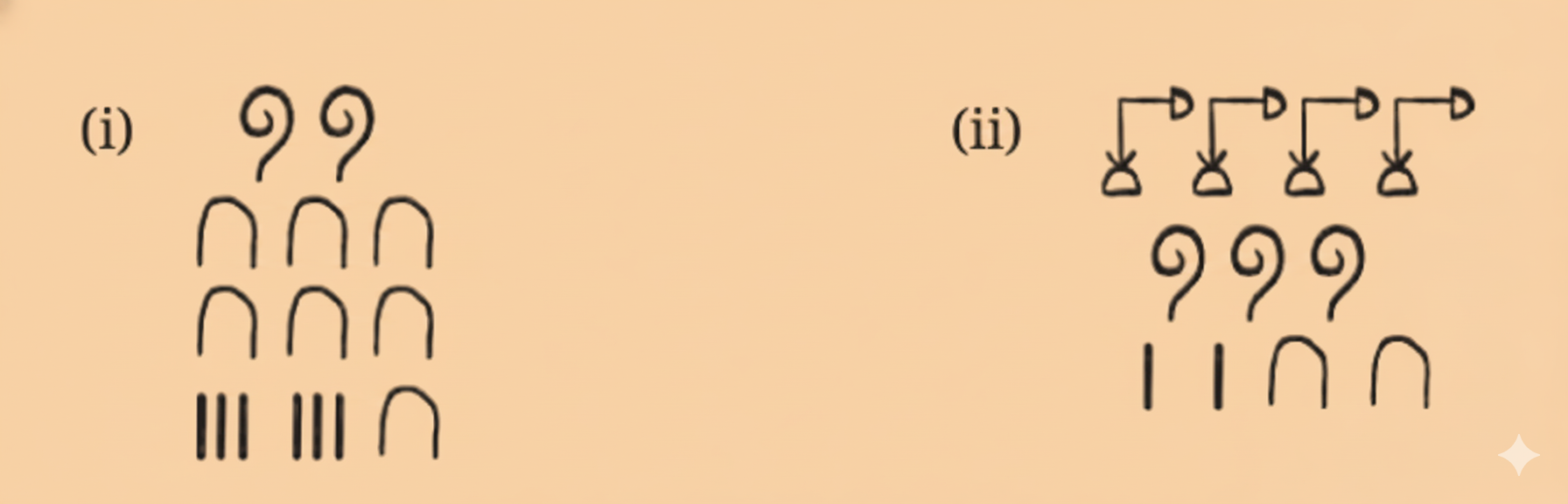Stepwise NCERT Solutions for Class 8 Maths Chapter 3 Exercises
Page 54 – Figure it Out
1. Suppose you are using the number system that uses sticks to represent numbers, as in Method 1. Without using either the number names or the numerals of the Hindu number system, give a method for adding, subtracting, multiplying and dividing two numbers or two collections of sticks.
Answer :
Method 1: Addition (Putting Together)
Take one set of sticks to represent the first number.
Take another set to represent the second number.
Combine both sets into a single group.
The total number of sticks in the group shows the sum.
Example:
Group A: |||| (4 sticks)
Group B: ||| (3 sticks)
Total: ||||||| → 7 sticks
Method 2: Subtraction (Taking Away)
Begin with the group of sticks representing the larger quantity.
Remove or take away the number of sticks representing the smaller quantity.
The sticks that remain show the difference.
Example:
Start with: ||||||| (7 sticks)
Take away: ||| (3 sticks)
Remaining: |||| → 4 sticks
Method 3: Multiplication (Repeated Addition)
Create several groups of sticks, each having the same number of sticks.
Count the total number of sticks across all groups.
The total represents the product.
Example:
3 groups of ||| (3 sticks each):
Group 1: |||
Group 2: |||
Group 3: |||
Total: ||||||||||| → 9 sticks
Method 4: Division (Equal Sharing or Grouping)
Take a total collection of sticks.
Either:
• Share equally into a fixed number of groups (to find how many in each group), or
• Group repeatedly by a set size (to find how many groups can be made).
Example (Equal Sharing):
Total: |||||| (6 sticks) ÷ 2 → ||| and ||| (3 sticks in each group)
Example (Grouping):
How many groups of || (2 sticks) can be made from |||||| (6 sticks)?
Answer: 3 groups
In short:
Addition means combining sticks,
Subtraction means taking away,
Multiplication means making equal groups repeatedly,
Division means sharing or grouping equally.
2. One way of extending the number system in Method 2 is by using strings with more than one letter — for example, we could use ‘aa’ for 27. How can you extend this system to represent all the numbers? There are many ways of doing it!
Answer : Treat the strings like a base-26 place-value system with letters as digits: a=1, b=2, …, z=26. After z, continue as two-letter “digits”: aa=27, ab=28, …, az=52, ba=53, …, zz=676, aaa=677, and so on. Other workable ideas exist, but the base-26 place-value approach is systematic and scales to any size.
3. Try making your own number system.
Answer: Example “ABC Number System” (base-5): Use five symbols A,B,C,D,E for 0–4. Positions follow powers of 5 (ones, fives, twenty-fives, …). Example: BD means 1×5 + 3 = 8. This shows how place value lets us write any whole number with just five symbols.
Page 59 – Figure it Out
1. Represent the following numbers in the Roman system. (i) 1222 (ii) 2999 (iii) 302 (iv) 715
Answer :
(i) 1222 → MCCXXII (1000 + 200 + 20 + 2)
(ii) 2999 → MMCMXCIX (2000 + 900 + 90 + 9)
(iii) 302 → CCCII (300 + 2)
(iv) 715 → DCCXV (700 + 10 + 5)
Page 60 – Figure it Out
1. A group of indigenous people in a Pacific island use different sequences of number names to count different objects. Why do you think they do this?
Answer: Because counting is tied to culture and use. Different objects (like fish, coconuts, people, days) may be grouped or valued differently, so special number words help classify, remember, or count in pairs/sets. Using separate sequences keeps meaning clear in daily life.
2. Consider the extension of the Gumulgal number system beyond 6 in the same way of counting by 2s. Come up with ways of performing the different arithmetic operations (+, –, ×, ÷) for numbers occurring in this system, without using Hindu numerals. Use this to evaluate the following:
(i)(ukasar-ukasar-ukasar-ukasar-urapon)+(ukasar-ukasar-ukasar-urapon)
(ii) (ukasar-ukasar-ukasar-ukasar-urapon) – (ukasar-ukasar-ukasar)
(iii) (ukasar-ukasar-ukasar-ukasar-urapon) × (ukasar-ukasar)
(iv)(ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar-ukasar) ÷ (ukasar-ukasar)
Answer: In Gumulgal, ukasar = 2 and urapon = 1. Add by joining 2s and 1s; subtract by removing; multiply by repeated joining; divide by making equal groups of ukasar.
(i) (2+2+2+2+1) + (2+2+2+1) = 9 + 7 = 16 → eight ukasar (i.e., ukasar repeated 8 times).
(ii) 9 − 6 = 3 → ukasar-urapon (2 + 1).
(iii) 9 × 4 = 36 → 18 copies of ukasar (since 36 is 18 twos).
(iv) 16 ÷ 4 = 4 → ukasar-ukasar (two twos).
3. Identify the features of the Hindu number system that make it efficient when compared to the Roman number system.
Answer: Place value, the use of zero, and just 10 symbols (0–9) allow compact writing and easy calculation. Large numbers stay short and operations like +, −, ×, ÷ follow simple rules—unlike Roman numerals, which are longer and harder to compute with.
4. Using the ideas discussed in this section, try refining the number system you might have made earlier.
Answer: Upgrade the system to a clear place-value base (e.g., base-5 with symbols A=0,…,E=4), make each position a power of the base, and include a zero symbol. This keeps numbers short, readable, and easy to calculate—similar to the Hindu system.
Page 62 – Figure it Out
1. Represent the following numbers in the Egyptian system: 10458, 1023, 2660, 784, 1111, 70707.
Answer :
2. What numbers do these numerals stand for?
Answer
(i) 100 + 100 + 10 + 10 + 10 + 10 + 10 + 10 + 10 + 1 + 1 + 1 + 1 + 1 + 1
= 200 + 70 + 6
= 276
(ii) 1000 + 1000 + 1000 + 1000 + 100 + 100 + 100 + 10 + 10 + 1 + 1
= 4000 + 300 + 20 + 2
= 4322
Page 63 – Figure it Out
1. Write the following numbers in the above base-5 system using the symbols in Table 2: 15, 50, 137, 293, 651.
Answer :
2. Is there a number that cannot be represented in our base-5 system above? Why or why not?
Answer :
No, every number can be represented in the base-5 system.
This is because:
The base-5 system uses five symbols (A, B, C, D, E) that represent the digits 0 to 4.
Any number can be expressed as a combination of these digits multiplied by powers of 5 (1, 5, 25, 125, and so on).
Since there is no limit to how many digits we can use, all whole numbers can be written in base-5.
3. Compute the landmark numbers of a base-7 system. In general, what are the landmark numbers of a base-n system?
Answer:
The landmark numbers in a base-7 system are the powers of 7:
7⁰ = 1
7¹ = 7
7² = 49
7³ = 343
7⁴ = 2401
7⁵ = 16807
…and so on.
In general, for a base-n number system, the landmark numbers are all powers of n — that is, n⁰, n¹, n², n³, and so forth. Each power represents a new place value in that number system.
:
1. Add the following Egyptian numerals:
Answer:
2. Add the following numerals that are in the base-5 system that we created:
Answer:
1. Can there be a number whose representation in Egyptian numerals has one of the symbols occurring 10 or more times? Why not?
Answer: No. The Egyptian system is additive and replaces ten of any symbol by a single symbol of the next higher value. So a symbol never needs to appear 10 or more times in a correct final writing.
2. Create your own number system of base 4 and represent numbers from 1 to 16.
Answer: Sample “Quad-Code” (base-4): A=0, B=1, C=2, D=3. Numbers 1→16: B, C, D, BA, BB, BC, BD, CA, CB, CC, CD, DA, DB, DC, DD, ABA. (Positions are powers of 4: 1, 4, 16, …)
3. Give a simple rule to multiply a given number by 5 in the base-5 system that we created.
Answer : Just append an A (zero) at the right end. In base-5 this shifts the number one place left, which multiplies it by 5. Example: BC (7) → BCA (7×5 = 35).
Page 73 – Figure it Out
1. Represent the following numbers in the Mesopotamian system — (i) 63 (ii) 132 (iii) 200 (iv) 60 (v) 3605
Answer :
Page 80 – Figure it Out
1. Why do you think the Chinese alternated between the Zong and Heng symbols? If only the Zong symbols were to be used, how would 41 be represented? Could this numeral be interpreted in any other way if there is no significant space between two successive positions?
Answer :
Why the Chinese alternated between Zong and Heng symbols:
The ancient Chinese numeral system used Zong (vertical) and Heng (horizontal) strokes to represent digits.
They alternated these two forms for each successive place value (units, tens, hundreds, etc.) so that the reader could easily distinguish one place from another.
This alternation made it visually clear where one number ended and the next began, especially when numbers were written close together on bamboo slips or narrow surfaces.
If only Zong symbols were used for 41:
41 = 4 tens + 1 unit.
Using only Zong (vertical) symbols:
→ Four Zongs for 4 tens and one Zong for 1 unit: IIII I
Problem with this representation:
Without alternating directions or leaving a visible space, IIII I could be mistaken for five Zongs, which equals 5, not 41.
Hence, the alternation of Zong and Heng was crucial for maintaining clear place value distinction.
In summary:
The Chinese alternated between Zong and Heng symbols to prevent confusion between different place values.
Without alternation or spacing, a number like 41 could easily be misinterpreted as 5.
2. Form a base-2 place value system using ‘ukasar’ and ‘urapon’ as the digits. Compare this system with that of the Gumulgal’s.
Answer :
Forming a Base-2 Place Value System using ‘ukasar’ and ‘urapon’:
To build a base-2 (binary) system, we assign the values:
‘ukasar’ = 0
‘urapon’ = 1
In this system, each position represents a power of 2, starting from the right:
1st place → 2⁰ = 1
2nd place → 2¹ = 2
3rd place → 2² = 4, and so on.
Examples:
1 → urapon
2 → urapon ukasar
3 → urapon urapon
4 → urapon ukasar ukasar
Each position tells how many of that power of 2 are used, with ‘ukasar’ marking a zero and ‘urapon’ marking a one.
Comparison with the Gumulgal System:
The Gumulgal number system is not a place value system. It works by adding groups of 2s and 1s — for example, to make 7, they might express it as ukasar-ukasar-ukasar-urapon (2 + 2 + 2 + 1).
In contrast, the base-2 system using ‘ukasar’ and ‘urapon’ is positional, meaning the value of each symbol depends on its place.
→ This makes it more efficient and systematic for representing larger numbers, while the Gumulgal additive method is simpler but limited to small values.
3. Where in your daily lives and in which professions, do the Hindu numerals and 0, play an important role? How might our lives have been different if our number system and 0 hadn’t been invented or conceived of?
Answer : We rely on Hindu numerals and zero for prices, time, phone numbers, banking, science, engineering, computers—almost everything. Without zero and place value, calculations would be slow and clumsy, large numbers hard to write, and modern technology would not have developed as it did.
4. The ancient Indians likely used base 10 for the Hindu number system because humans have 10 fingers and so we can use our fingers to count. But what if we had only 8 fingers? How would we be writing numbers then? What would the Hindu numerals look like if we were using base 8 instead? Base 5? Try writing the base-10 Hindu numeral 25 as base-8 and base-5 Hindu numerals, respectively. Can you write it in base-2?
Answer :
If humans had only 8 fingers:
We would most likely have developed a base-8 (octal) number system instead of base-10. In such a system, counting would go from 0 to 7, and all calculations would be based on powers of 8. Our numerals and arithmetic methods would have evolved accordingly, just as today’s Hindu numerals are built around base-10.
Converting the base-10 number 25 into other bases:
► Base-8 (Octal):
25 ÷ 8 = 3 remainder 1
3 ÷ 8 = 0 remainder 3
So, 25₁₀ = 31₈
► Base-5 (Quinary):
25 ÷ 5 = 5 remainder 0
5 ÷ 5 = 1 remainder 0
1 ÷ 5 = 0 remainder 1
So, 25₁₀ = 100₅
► Base-2 (Binary):
25 ÷ 2 = 12 remainder 1
12 ÷ 2 = 6 remainder 0
6 ÷ 2 = 3 remainder 0
3 ÷ 2 = 1 remainder 1
1 ÷ 2 = 0 remainder 1
So, 25₁₀ = 11001₂
Summary:
If we had 8 fingers, our everyday number system would likely use base 8, with digits 0–7. For the number 25 (in base 10):
In base-8, it’s 31
In base-5, it’s 100
In base-2, it’s 11001
NCERT Solutions Class 8 Maths Chapter 3 A Story of Numbers 2025-26
Mastering Class 8 Maths Chapter 3 A Story of Numbers is essential for building a strong foundation in arithmetic and number patterns. Our step-by-step NCERT solutions for 2025-26 are designed to make concepts easy and exam-ready for every learner.
By practicing these NCERT Class 8 chapter-wise solutions, you can boost your problem-solving ability and tackle tricky questions with confidence. Focus on understanding place value, properties of numbers, and patterns for top performance in your assessments.
Consistent revision using chapter exercises helps in quick recall and effective learning. Remember to review solved examples and practice regularly to strengthen your basics and score maximum marks in your exams.
FAQs on Class 8 Maths Chapter 3 NCERT Solutions: A Story of Numbers
1. What are NCERT Solutions for Class 8 Maths Chapter 3: A Story of Numbers, and how do they help in CBSE 2025–26 exams?
NCERT Solutions for Class 8 Maths Chapter 3: A Story of Numbers provide detailed, stepwise answers for all textbook exercises, adhering strictly to the CBSE 2025–26 syllabus and marking scheme. Using these solutions builds a strong conceptual foundation, enhances exam writing skills, and maximizes your marks in school assessments and final exams by clarifying every step in problem-solving.
2. How should I write stepwise NCERT answers in Chapter 3 to score full marks in Class 8 Maths?
To score full marks using the NCERT Solutions for Class 8 Maths Chapter 3, always structure your answers stepwise as shown below:
- Read the question carefully and underline key terms.
- State any formulas or definitions used.
- Show all calculation steps clearly, without skipping any logical transitions.
- Box the final answer and write it neatly.
- Review your answer for accuracy and completeness before submission.
3. Which types of questions from Class 8 Maths Chapter 3 are most important for CBSE board exams?
In Class 8 Maths Chapter 3: A Story of Numbers, high-priority questions for exams typically include application-based questions, conceptual reasoning, short formula-based sums, and problems involving number properties. Focusing on these promotes better marks as they closely align with CBSE’s current exam trends and marking patterns.
4. Are diagrams or definitions mandatory in NCERT Solutions for Class 8 Maths Chapter 3 answers?
Including well-labelled diagrams and accurate definitions, where required, in your NCERT Solutions for Class 8 Maths Chapter 3 answers can substantially increase your marks. Some questions explicitly ask for diagrams, while others benefit from clear definitions—always refer to Vedantu's solutions for model answers and best practices.
5. How can I structure long answers in Class 8 Maths Chapter 3 for maximum CBSE marks?
Long answers in the NCERT Solutions for Class 8 Maths Chapter 3 should be presented as follows:
- Start with a brief introduction or definition relevant to the topic.
- Use bullets or short paragraphs for each logical point.
- Include diagrams or examples if appropriate.
- Finish with a concise summary or final statement boxed or underlined.
- Maintain clear handwriting and neat formatting throughout.
6. Where can I download the free PDF of NCERT Solutions for Class 8 Maths Chapter 3 – A Story of Numbers?
You can download the free PDF of NCERT Solutions for Class 8 Maths Chapter 3 – A Story of Numbers exclusively from Vedantu. This PDF contains comprehensive, exercise-wise, stepwise solutions, making offline revision easy and effective for CBSE exams.
7. Do examiners award partial marks for correct steps in Class 8 Maths Chapter 3 even if the final answer is wrong?
Yes, CBSE examiners often award partial marks in Class 8 Maths Chapter 3 if you show the correct steps even when the final answer is incorrect. Following the stepwise approach outlined in Vedantu’s NCERT Solutions increases your chance of securing partial credit for method accuracy.
8. Are NCERT Solutions enough for Class 8 Maths Chapter 3 exam preparation, or should I use additional resources?
NCERT Solutions for Class 8 Maths Chapter 3 cover all essential concepts and question types required for CBSE 2025–26 exams. For thorough preparation, practice all solved and unsolved exercises first. After that, refer to Vedantu's revision notes or exemplar solutions for extra practice on tricky problems.
9. What are some common mistakes students make in Class 8 Maths Chapter 3 and how can they be avoided?
Avoiding frequent errors in NCERT Solutions for Class 8 Maths Chapter 3 is crucial for scoring well. Watch out for:
- Missing key steps in calculations.
- Ignoring units or mislabelling diagrams.
- Using incorrect formulae or definitions.
- Rushing through word problems without analyzing requirements.
- Forgetting to revise answers for accuracy.
10. How can I revise Class 8 Maths Chapter 3 quickly using Vedantu’s NCERT Solutions for board exams?
For rapid revision of NCERT Solutions for Class 8 Maths Chapter 3, follow these steps:
- Read through solved examples and chapter summaries.
- Attempt back exercise questions without referring to solutions.
- Use Vedantu’s revision planner (1-day, 3-day, 7-day) with flash notes for key concepts.
- Review common mistakes and marking scheme insights.
11. How do references to textbook page numbers assist in revising NCERT Solutions for Class 8 Maths Chapter 3?
Including textbook page numbers when using NCERT Solutions for Class 8 Maths Chapter 3 helps you cross-check with original explanations. This ensures you don’t miss context, allows for deeper understanding, and streamlines last-minute revision by quickly locating exact concepts and worked examples.
12. What is the best way to use chapterwise solutions for Class 8 Maths Chapter 3 from Vedantu for exam preparation?
For optimal exam preparation with NCERT Solutions for Class 8 Maths Chapter 3 from Vedantu, approach each exercise systematically. Begin by understanding the concept, solve practice questions independently, compare with Vedantu’s stepwise answers, and make a note of any gaps in your understanding for targeted revision. Regular practice fosters confidence and ensures exam readiness.
