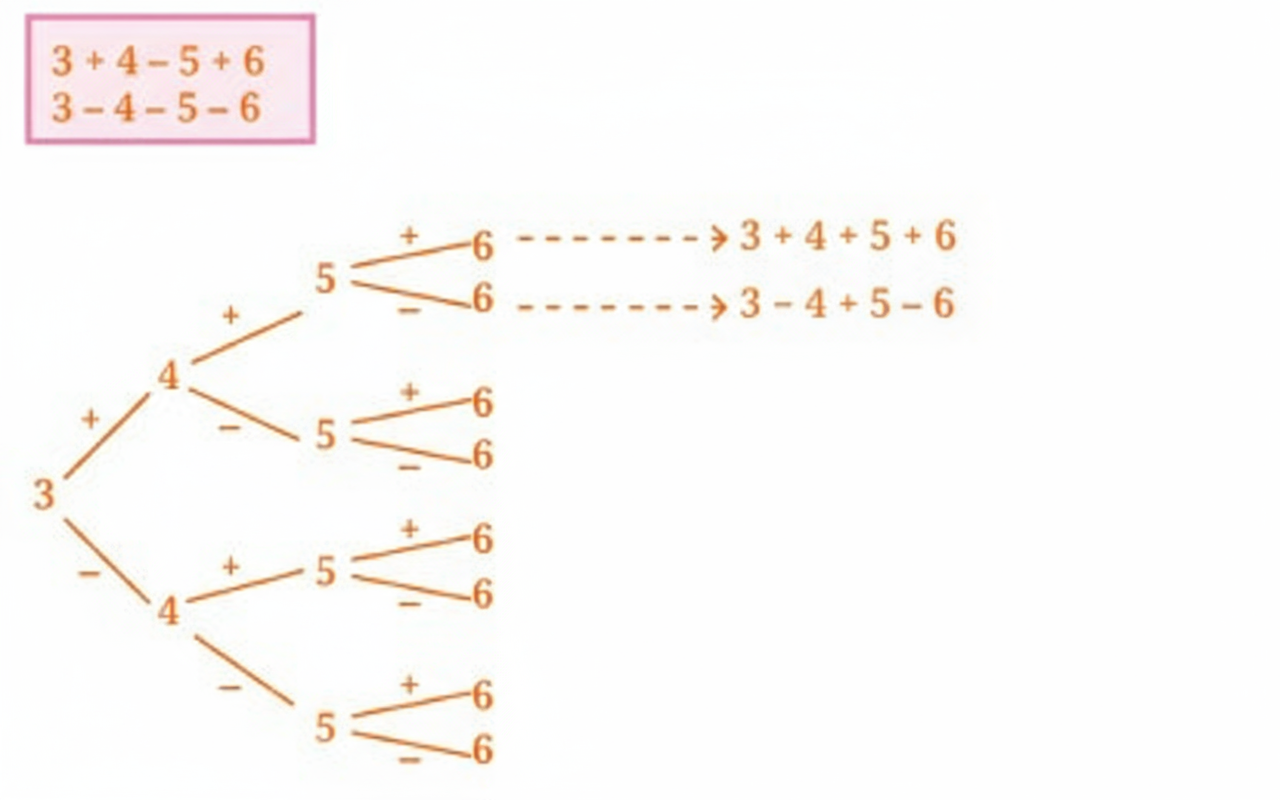
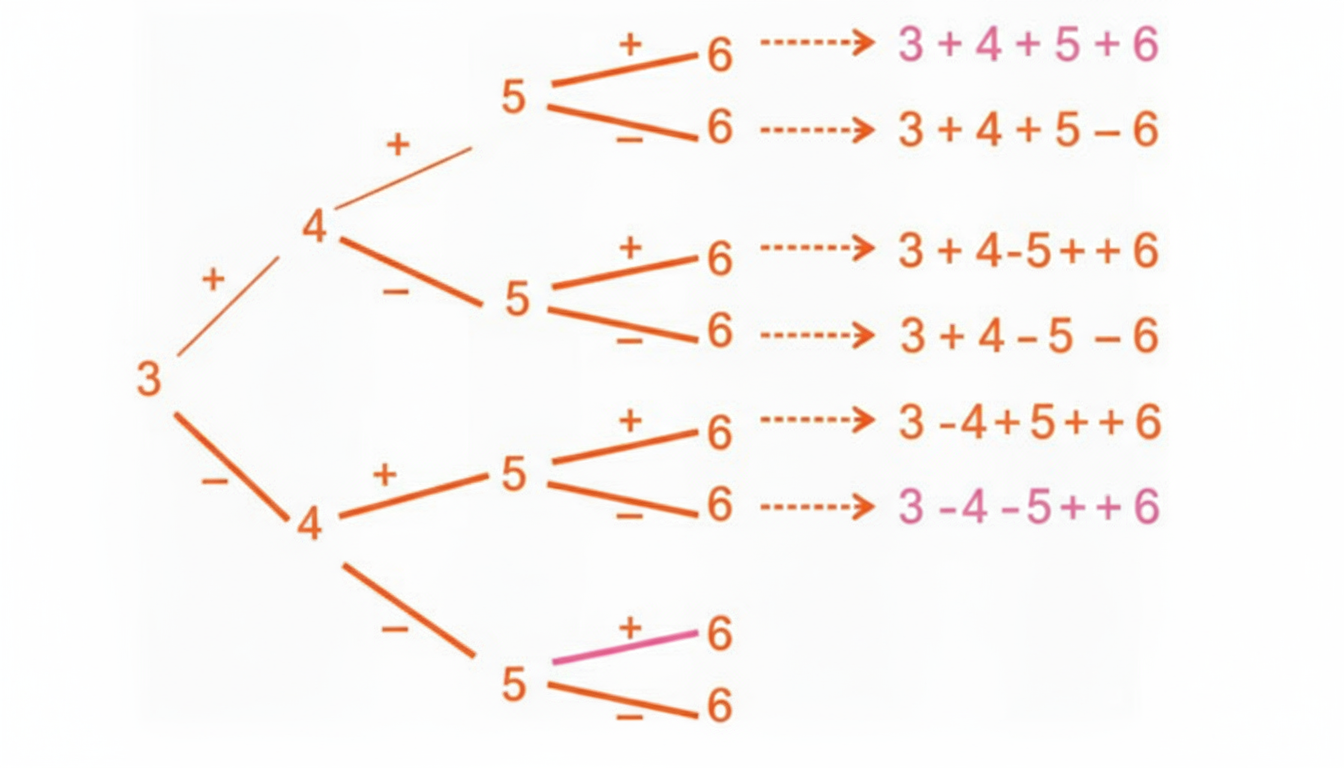
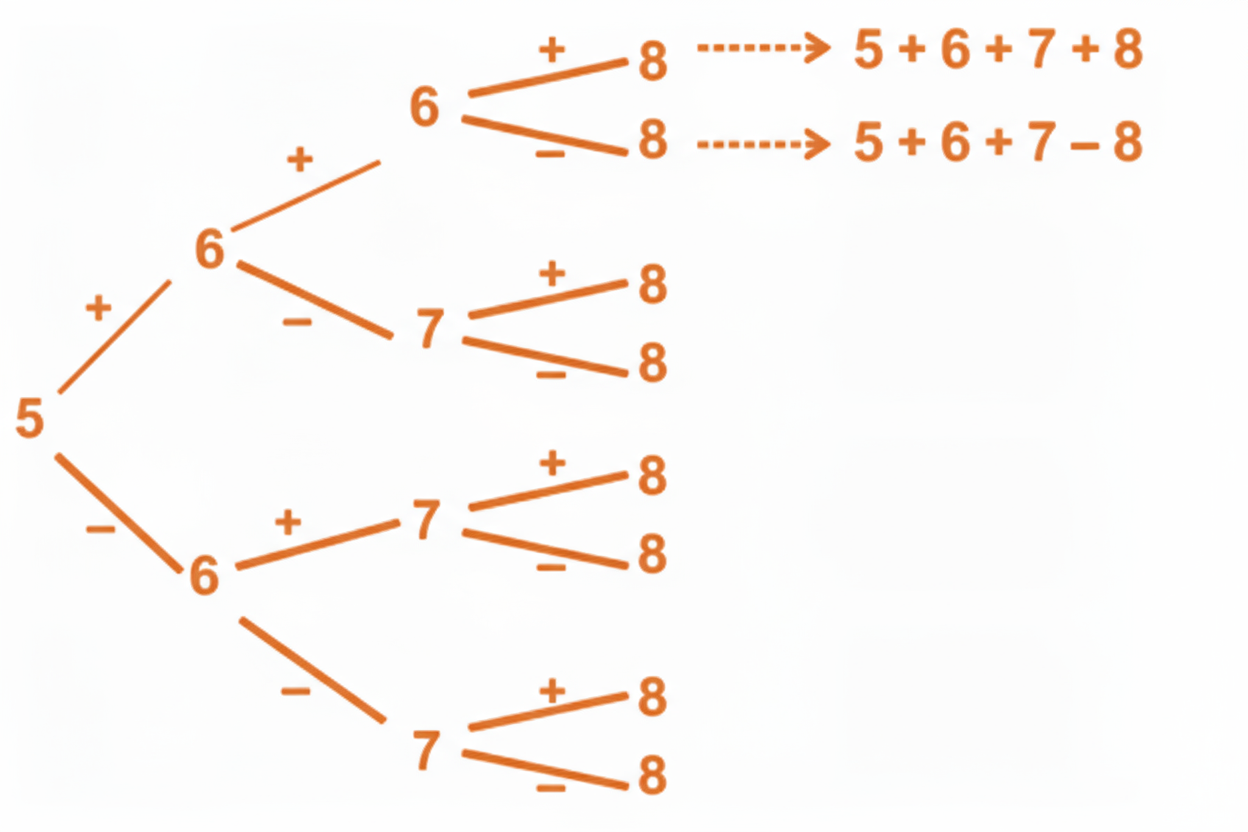
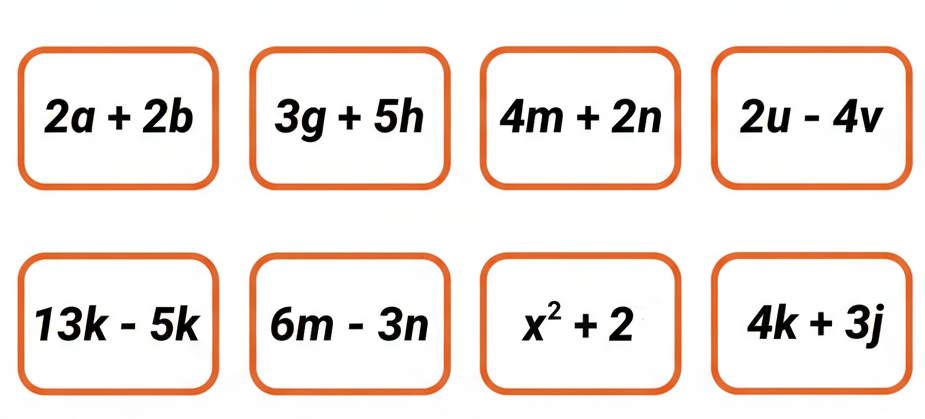
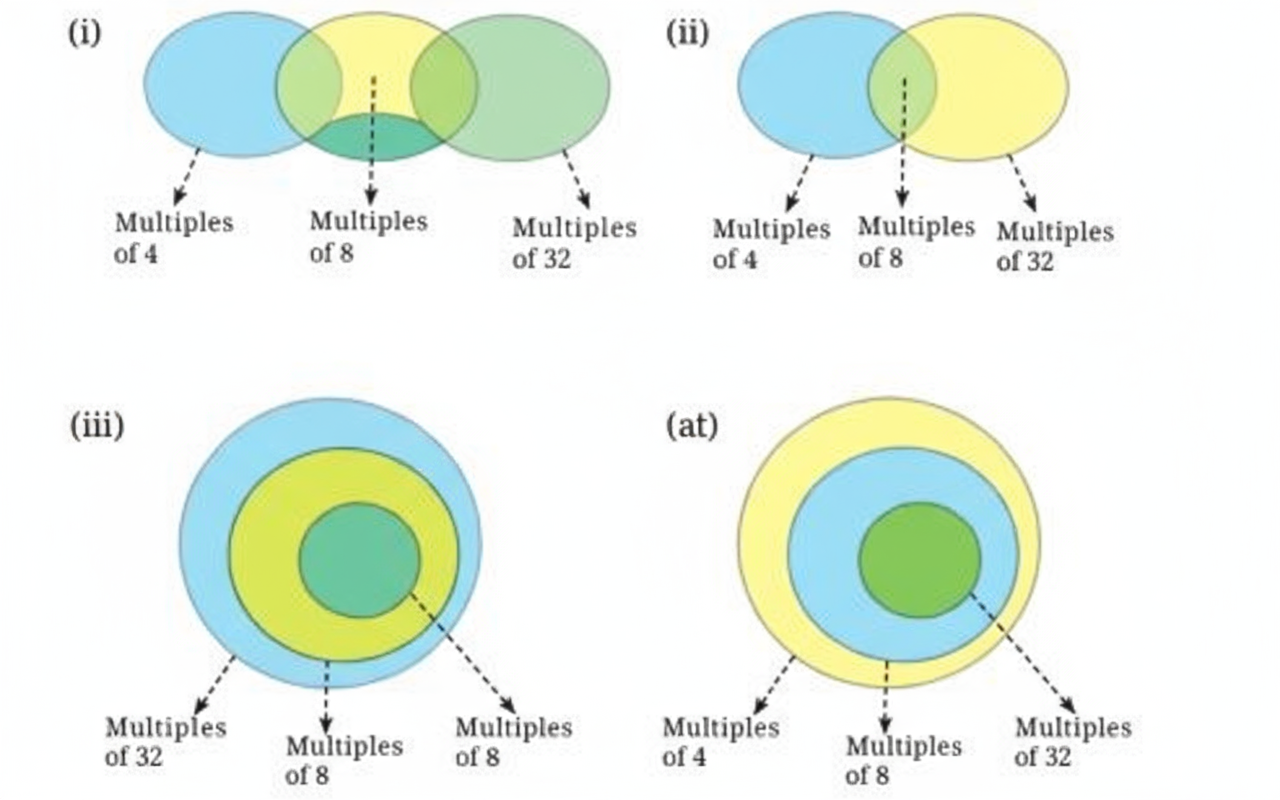
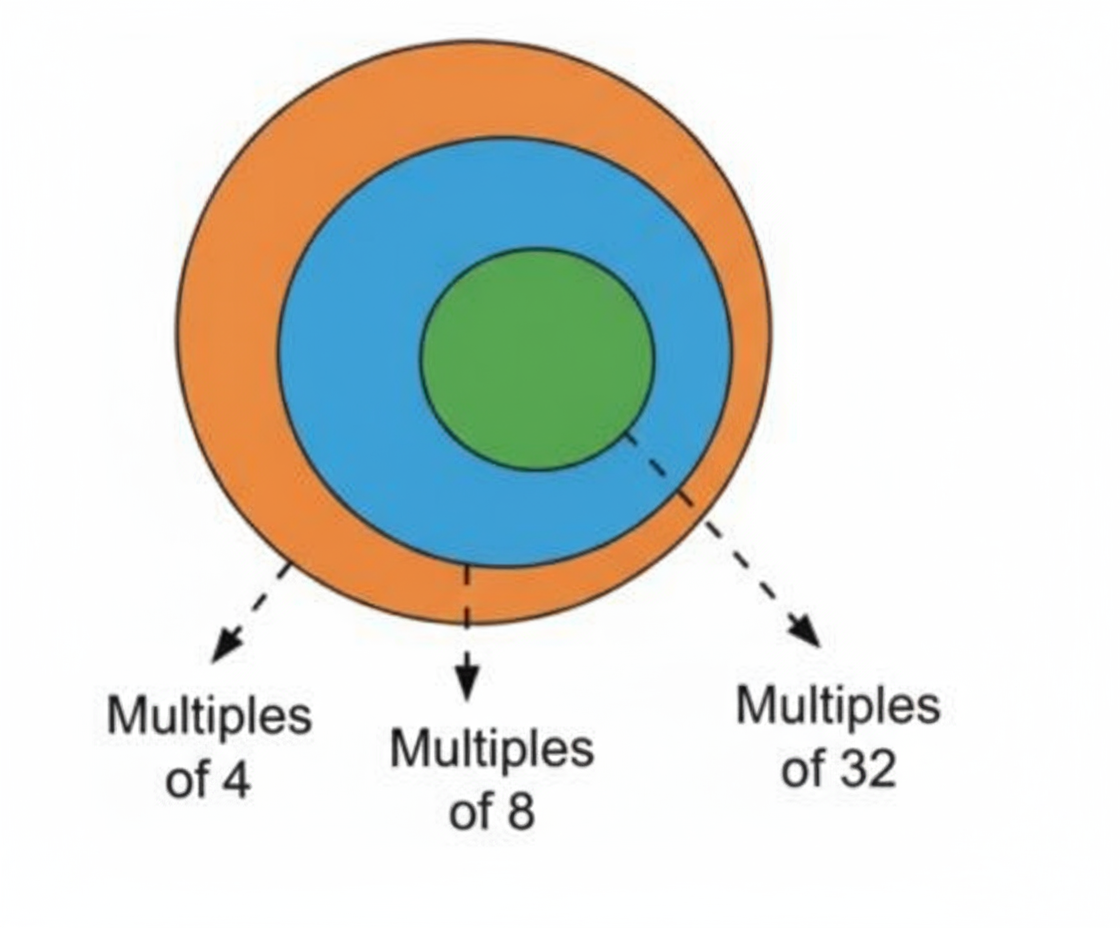
How to Write Perfect Answers for Number Play in Class 8 Maths
1. Take any 4 consecutive numbers. For example, 3, 4, 5, and 6. Place ‘+’ and signs in between the numbers. How many different possibilities exist? Write all of them.
Evaluate each expression and write the result next to it. Do you notice anything interesting?
Answer:
When four consecutive numbers are combined using all possible ‘+’ and ‘–’ sign arrangements, the final result will always be an even number. This happens because no matter how the signs are placed, the addition and subtraction balance out evenly across consecutive numbers. In particular, the sum of four consecutive numbers is always even, and the differences between them also produce even results when combined with plus and minus signs.
Example using 3, 4, 5, and 6:
3 + 4 + 5 + 6 = 18
3 + 4 + 5 – 6 = 6
3 + 4 – 5 + 6 = 8
3 + 4 – 5 – 6 = -4
3 – 4 + 5 + 6 = 10
3 – 4 + 5 – 6 = -2
3 – 4 – 5 + 6 = 0
3 – 4 – 5 – 6 = -12
Observations:
All the results are even numbers.
There are eight possible combinations in total.
The outcomes can be positive, negative, or zero.
2. Now, take four other consecutive numbers. Place the ‘+’ and ‘-’ signs as you have done before. Find out the results of each expression. What do you observe?
Answer:
Let us take numbers 5, 6, 7, 8:
Now,
5 + 6 + 7 + 8 = 26
5 + 6 + 7 – 8 = 10
5 + 6 – 7 + 8 = 12
5 + 6 – 7 – 8 = -4
5 – 6 + 7 + 8 = 14
5 – 6 + 7 – 8 = -2
5 – 6 – 7 + 8 = 0
5 – 6 – 7 – 8 = -16
Conclusion:
No matter which four consecutive numbers are chosen, using all possible combinations of plus and minus signs always gives even results.
This happens because the total sum and differences of consecutive numbers always produce even outcomes, regardless of the sign arrangement.’
Intext Questions:
Using our understanding of how parity behaves under different operations, identify which of the following algebraic expressions give an even number for any integer values for the letter-numbers.
1. 2a + 2b
2. 3g + 5h
3. 4m + 2n
4. 2u – 4v
5. 13k – 5k
6. 6m – 3n
7. x2 + 2
8. b2 + 1
9. 4k × 3j
Answer:
1. Expression: 2a + 2b
2a is even because it’s a multiple of 2.
2b is also even as it’s a multiple of 2.
The sum of two even numbers is always even.
∴ 2a + 2b is always even.
Expression: 3g + 5h
If both g and h are odd → 3g and 5h are odd → sum is even.
Example: 3×1 + 5×1 = 8 (even)If both g and h are even → 3g and 5h are even → sum is even.
Example: 3×2 + 5×2 = 16 (even)If g is odd and h is even → 3g is odd, 5h is even → sum is odd.
Example: 3×1 + 5×2 = 13 (odd)
∴ 3g + 5h is not always even.
Expression: 4m + 2n
4m is even (multiple of 2).
2n is even (multiple of 2).
Sum of two even numbers is even.
∴ 4m + 2n is always even.
Expression: 2u – 4v
2u and 4v are both even.
Difference of two even numbers is even.
∴ 2u – 4v is always even.
Expression: 13k – 5k
Simplifies to 8k.
8k is even as it’s a multiple of 2.
∴ 13k – 5k is always even.
Expression: 6m – 3n
6m is always even.
3n may be even or odd, depending on n.
If n is odd → 3n is odd → even – odd = odd.
Example: 6×1 – 3×1 = 3 (odd)
∴ 6m – 3n is not always even.
Expression: x² + 2
If x² is even → x² + 2 is even.
If x² is odd → x² + 2 is odd.
∴ x² + 2 is not always even.
Expression: b² + 1
If b is even → b² is even → b² + 1 is odd.
Example: 2² + 1 = 5 (odd)If b is odd → b² is odd → b² + 1 is even.
Example: 3² + 1 = 10 (even)
∴ b² + 1 is not always even.
Expression: 4k × 3j
Simplifies to 12kj.
12kj is even because it’s a multiple of 2.
∴ 4k × 3j is always even.
Figure It Out (Pages 122-123)
Question 1.
The sum of four consecutive numbers is 34. What are these numbers?
Answer:
Let the four consecutive numbers be x, x + 1, x + 2, and x + 3.
So,
x + (x + 1) + (x + 2) + (x + 3) = 34
⇒ 4x + 6 = 34
⇒ 4x = 34 – 6 = 28
⇒ x = 7
Hence, the four numbers are:
x = 7,
x + 1 = 8,
x + 2 = 9,
x + 3 = 10.
✅ Therefore, the consecutive numbers are 7, 8, 9, and 10.
2. Suppose p is the greatest of five consecutive numbers. Describe the other four numbers in terms of p.
Answer:
If p is the largest among five consecutive numbers, then the remaining four numbers will be:
(p – 1), (p – 2), (p – 3), and (p – 4).
Here,
(p – 1) is the 2nd largest number,
(p – 2) is the 3rd largest number,
(p – 3) is the 4th largest number,
(p – 4) is the smallest number.
Hence,
p > (p – 1) > (p – 2) > (p – 3) > (p – 4).
3. For each statement below, determine whether it is always true, sometimes true, or never true. Explain your answer. Mention examples and non-examples as appropriate. Justify your claim using algebra.
(i) The sum of two even numbers is a multiple of 3.
Answer:
✅ Sometimes true.
Example:
2 + 4 = 6, 8 + 10 = 18, and 14 + 16 = 30 → all are multiples of 3.
But, 2 + 6 = 8 and 4 + 10 = 14 → not multiples of 3.
(ii) If a number is not divisible by 18, then it is also not divisible by 9.
Answer:
✅ Sometimes true.
Example:
27 is not divisible by 18, but it is divisible by 9 → True.
40 is not divisible by 18, and it is not divisible by 9 → False.
(iii) If two numbers are not divisible by 6, then their sum is not divisible by 6.
Answer:
❌ Never true.
Example:
8 and 10 are not divisible by 6, but 8 + 10 = 18 → divisible by 6.
10 and 13 are not divisible by 6, and 10 + 13 = 23 → not divisible by 6.
So, it doesn’t hold in all cases.
(iv) The sum of a multiple of 6 and a multiple of 9 is a multiple of 3.
Answer:
✅ Always true.
Let multiples be 6m and 9n.
Then, 6m + 9n = 3(2m + 3n), which is always divisible by 3.
(v) The sum of a multiple of 6 and a multiple of 3 is a multiple of 9.
Answer:
✅ Sometimes true.
Multiples of 6: 6, 12, 18, 24, 30,…
6 + 12 = 18 → multiple of 9
12 + 18 = 30 → not a multiple of 9
Multiples of 3: 3, 6, 9, 12, 15,…
3 + 6 = 9 → multiple of 9
6 + 9 = 15 → not a multiple of 9
Hence, this statement is sometimes true.
4. Find a few numbers that leave a remainder of 2 when divided by 3 and a remainder of 2 when divided by 4. Write an algebraic expression to describe all such numbers.
Answer:
If dividing by 3 leaves remainder 2, the number has the form 3K + 2 where K = 1,2,3,…
K = 1 → 3×1 + 2 = 5
K = 2 → 3×2 + 2 = 8
K = 3 → 3×3 + 2 = 11
So 5, 8, 11,… leave remainder 2 on division by 3. Algebraic expression: 3K + 2.
If dividing by 4 leaves remainder 2, the number has the form 4K + 2 where K = 1,2,3,…
K = 1 → 4×1 + 2 = 6
K = 2 → 4×2 + 2 = 10
K = 3 → 4×3 + 2 = 14
So 6, 10, 14,… leave remainder 2 on division by 4. Algebraic expression: 4K + 2.
5. “I hold some pebbles, not too many, when I group them in 3’s, one stays with me. Try pairing them up — it simply won’t do. A stubborn odd pebble remains in my view. Group them by 5, yet one’s still around, but grouping by seven, perfection is found. More than one hundred would be far too bold. Can you tell me the number of pebbles I hold?”
Answer:
The count is 1 more than multiples of 3 and 5, and a multiple of 7. The LCM of 3, 5, 7 is 105, so the smallest such number is 105 + 1 = 106. Thus, there are 106 pebbles.
6. Tathagat has written several numbers that leave a remainder of 2 when divided by 6. He claims, “If you add any three such numbers, the sum will always be a multiple of 6.” Is Tathagat’s claim true?
Answer:
Such numbers are of the form 6k + 2: 8, 14, 20, 26, …
8 + 14 + 20 = 42 (multiple of 6)
14 + 20 + 26 = 60 (multiple of 6)
Hence, the claim is true: the sum of any three numbers of the form 6k+2 is divisible by 6.
7. When divided by 7, the number 661 leaves a remainder of 3, and 4779 leaves a remainder of 5. Without calculating, can you say what remainders the following expressions will leave when divided by 77? Show the solution both algebraically and visually.
(i) 4779 + 661
(ii) 4779 – 661
Answer:
Algebraic idea (mod 7): 4779 ≡ 5, 661 ≡ 3.
(i) 5 + 3 = 8 ≡ 1 (mod 7) → remainder 1
(ii) 5 − 3 = 2 (mod 7) → remainder 2
Visualisation:
(i) 4779 + 661 = 7(682 + 94) + (5 + 3) = 7·776 + 8 ⇒ remainder 1
(ii) 4779 − 661 = 7(682 − 94) + (5 − 3) = 7·588 + 2 ⇒ remainder 2
8. Find a number that leaves a remainder of 2 when divided by 3, a remainder of 3 when divided by 4, and a remainder of 4 when divided by 5. What is the smallest such number? Can you give a simple explanation of why it is the smallest?
Answer:
Forms:
By 3: 3K + 2 → 5, 8, 11, 14, 17, 20, …
By 4: 4K + 3 → 7, 11, 15, 19, …
By 5: 5K + 4 → 9, 14, 19, 24, …
The smallest number fitting all three at once is 59. Since LCM(3,4,5) = 60, a number that is 1 less than 60 (i.e., 59) gives remainders 2, 3, and 4 respectively, and is therefore minimal.
Figure It Out (Page 126)
1. Find, without dividing, whether the following numbers are divisible by 9.
(i) 123 (ii) 405 (iii) 8888 (iv) 93547 (v) 358095
Answer:
Rule: a number is divisible by 9 if its digit-sum is divisible by 9.
(i) 1+2+3=6 → not divisible
(ii) 4+0+5=9 → divisible
(iii) 8+8+8+8=32 → not divisible
(iv) 9+3+5+4+7=28 → not divisible
(v) 3+5+8+0+9+5=30 → not divisible
2. Find the smallest multiple of 9 with no odd digits.
Answer:
The smallest multiple of 9 whose digits are all even is 288 (2,8,8 are even; 2+8+8=18, a multiple of 9).
3. Find the multiple of 9 that is closest to the number 6000.
Answer:
Digit-sum of 6000 is 6, so it’s not a multiple of 9. Adding 3 gives 6003, which is a multiple of 9. Hence the closest (per the given method) is 6003.
4. How many multiples of 9 are there between the numbers 4300 and 4400?
Answer:
They run from 4302 to 4392: 4302, 4311, …, 4392.
Count = (4392 − 4302)/9 + 1 = 10 + 1 = 11.
Intext Questions (Pages 130)”
1. Between the numbers 600 and 700, which numbers have the digital root:
(i) 5 (ii) 7 (iii) 3
Answer:
(i) DR = 5: 608, 617, 662, 689, …
(ii) DR = 7: 610, 619, 637, 673, …
(iii) DR = 3: 606, 615, 633, 678, …
2. Write the digital roots of any 12 consecutive numbers. What do you observe?
Answer:
Example 105–116 → 6, 7, 8, 9, 1, 2, 3, 4, 5, 6, 7, 8.
Observation: The pattern repeats every 9 numbers (cycle 1–9). Also, multiples of 9 have digital root 9 (e.g., 405, 234, 1035, 936 → 9).
3. We saw that the digital root of multiples by 9 is always 9. Now, find the digital roots of some consecutive multiples of (i) 3, (ii) 4, and (iii) 6.
Answer:
(i) Multiples of 3 → DR pattern: 3, 6, 9, 3, 6, 9, …
(ii) Multiples of 4 → DR pattern: 5, 9, 4, 8, 3, 7, 2, 6, …
(iii) Multiples of 6 → DR pattern: 3, 9, 6, 3, 9, 6, …
4. What are the digital roots of numbers that are 1 more than a multiple of 6? What do you notice? Try to explain the patterns noticed.
Answer:
Examples: 37 → 1, 43 → 7, 49 → 4, 55 → 1, 61 → 7, 67 → 4, …
So the cycle is 1, 7, 4, 1, 7, 4, …
5. I’m made of digits, each tiniest and odd, No shared ground with root #1 – how odd!
My digits count, their sum, my root – All point to one bold number’s pursuit – The largest odd single-digit I proudly claim. What’s my number? What’s my name?
Answer:
111 111 111 (nine 1’s): all digits odd; 9 digits; sum = 9; digital root = 9. All conditions are met.
Figure It Out (Page 131)
1. The digital root of an 8-digit number is 5. What will be the digital root of 10 more than that number?
Answer:
Adding 10 generally increases the digit-sum by 1, so the digital root moves from 5 to 6 (e.g., 80000006 → 80000016).
2. Write any number. Generate a sequence of numbers by repeatedly adding 11. What would be the digital roots of this sequence of numbers? Share your observations.
Answer:
Starting at 40, digital roots are: 4, 6, 8, 1, 3, 5, 7, 9, 2, 4, …
Observation: The pattern repeats every 9 steps.
3. What will be the digital root of the number 9a + 36b + 13?
Answer:
Multiples of 9 contribute digital root 9 (0 mod 9). So DR(9a + 36b + 13) = DR(9 + 4) = DR(13) = 4. Checks with sample values confirm this.
4. Make conjectures by examining if there are any patterns or relations between (i) the parity of a number and its digital root. (ii) the digital root of a number and the remainder obtained when the number is divided by 3 or 9.
Answer:
(i) No fixed connection: even numbers may have odd or even digital roots (e.g., 16 → DR 7; 40 → DR 4).
(ii) Remainders: modulo 3, the remainder equals DR mod 3; modulo 9, the remainder equals DR (with DR=9 meaning remainder 0).
5.3 Digits in Disguise (Pages 132–134)
1. If 31z5 is a multiple of 9, where z is a digit, what is the value of z? Explain why there are two answers to this problem.
Answer:
Digit-sum = 3 + 1 + z + 5 = 9 + z must be a multiple of 9 ⇒ z = 0 or z = 9. Hence two answers.
2. “I take a number that leaves a remainder of 8 when divided by 12.1 take another number, which is 4 short of a multiple of 12. Their sum will always be a multiple of 8”, claims Snehal. Examine his claim and justify your conclusion.
Answer:
Let the numbers be 12k + 8 and 12m − 4. Their sum is 12(k+m) + 4 = 4[3(k+m)+1], always a multiple of 4, but not necessarily of 8. So the claim is not always true.
3. When is the sum of two multiples of 3, a multiple of 6, and when is it not? Explain the different possible cases, and generalise the pattern.
Answer:
Let them be 3a and 3b. Sum = 3(a+b). For divisibility by 6, the sum must be even ⇒ a+b even. Thus, two “even-indexed” or two “odd-indexed” multiples of 3 give a multiple of 6; one of each does not.
4. Sreelatha says, “I have a number that is divisible by 9. If I reverse its digits, it will still be divisible by 9”. (i) Examine if her conjecture is true for any multiple of 9. (ii) Are any other digit shuffles possible such that the number formed is still a multiple of 9?
Answer:
(i) True — reversing doesn’t change the digit-sum.
(ii) Yes — any permutation preserves divisibility by 9.
5. If 48a23b is a multiple of 18, list all possible pairs of values for a and b.
Answer:
For a multiple of 18, the number must be divisible by 2 and 9. Thus, b is even and 4+8+a+2+3+b = 17+a+b is a multiple of 9. From the given approach, examples that work are: (a,b) = (1,0) and (4,6).
Question 6. If 3p7q8 is divisible by 44, list all possible pairs of values for p and q.
Answer:
A number divisible by 44 must be divisible by 4 and 11. The solution’s trials yield the following pairs: (7,0), (5,2), (3,4), (1,6).
7. Find three consecutive numbers such that the first number is a multiple of 2, the second number is a multiple of 3, and the third number is a multiple of 4. Are there more such numbers? How often do they occur?
Answer:
Examples: (2,3,4), (14,15,16), (26,27,28), (38,39,40). There are infinitely many; such triples appear every 12 numbers.
8. Write five multiples of 36 between 45,000 and 47,000. Share your approach with the class.
Answer:
Since 36 = 4×9, check divisibility by 4 and 9. Starting from 45,000 and adding 36 repeatedly gives: 45,036; 45,072; 45,108; 45,144; 45,180.
9. The middle number in the sequence of 5 consecutive even numbers is 5p. Express the other four numbers in sequence in terms of p.
Answer:
The five even numbers are: 5p − 4, 5p − 2, 5p, 5p + 2, 5p + 4.
10. Write a 6-digit number that is divisible by 15, such that when the digits are reversed, it is divisible by 6.
Answer:
Example: 643215 is divisible by 15 (sum 21; ends in 5). Reversing gives 512346, which is divisible by 6 (even; sum 21).
11. Deepak claims, “There are some multiples of 11 which, when doubled, are still multiples of 11. But other multiples of 11 don’t remain multiples of 11 when doubled”. Examine if his conjecture is true; explain your conclusion.
Answer:
Every multiple of 11 is 11k. Doubling gives 22k = 11(2k), still a multiple of 11. So the claim is false.
12. Determine whether the statements below are ‘Always True’, ‘Sometimes True’, or ‘Never True’. Explain your reasoning.
(i) The product of a multiple of 6 and a multiple of 3 is a multiple of 9.
(ii) The sum of three consecutive even numbers will be divisible by 6.
(iii) If abcdef is a multiple of 6, then badcef will be a multiple of 6.
(iv) 8(7b – 3) – 4(11b + 1) is a multiple of 12.
Answer:
(i) Always True: (6a)(3b) = 18ab, a multiple of 9.
(ii) Always True: 2n + (2n+2) + (2n+4) = 6(n+1).
(iii) Always True: Reordering preserves digit-sum (mod 3) and the last digit (even/odd), so divisibility by 6 remains.
(iv) Sometimes True: 8(7b−3) − 4(11b+1) = 12b − 28 = 4(3b−7); multiple of 12 only for suitable b.
13. Choose any 3 numbers. When is their sum divisible by 3? Explore all possible cases and generalise.
Answer:
Let remainders mod 3 be r1, r2, r3 ∈ {0,1,2}. The sum is divisible by 3 iff r1+r2+r3 is a multiple of 3 — i.e., either all three are the same, or all three are different (0,1,2).
14. Is the product of two consecutive integers always a multiple of 2? Why? What about the product of these consecutive integers? Is it always a multiple of 6? Why or why not? What can you say about the product of 4 consecutive integers? What about the product of five consecutive integers?
Answer:
Two consecutive integers: one is even ⇒ product is always a multiple of 2.
Not always a multiple of 6 (only when one factor is a multiple of 3).
Four consecutive integers: examples show divisibility by 12 (e.g., 2·3·4·5 = 120).
Five consecutive integers: examples show divisibility by 24 (e.g., 1·2·3·4·5 = 120).
15. Solve the cryptarithms (i) EF × E = GGG (ii) WOW × 5 = MEOW
Answer:
(i) Example solution: 37 × 3 = 111 → fits EF × E = GGG.
(ii) Example solution: 525 × 5 = 2625 → fits WOW × 5 = MEOW.
16. Which of the following Venn diagrams captures the relationship between the multiples of 4, 8, and 32?
Answer:
Multiples of 4 are: 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64,…
Multiples of 8 are: 8, 16, 24, 32, 40, 48, 56, 64,…
Multiples of 32 are: 32, 64, 96, 128,…
The relationship between these sets of multiples can be clearly represented using a Venn diagram, where the multiples of 32 fall entirely within the set of multiples of 8, and the multiples of 8 fall entirely within the set of multiples of 4.”
Universal Franchise and India's Electoral System – Key Concepts Explained
Grasping the idea of a universal adult franchise is crucial to understanding Indian democracy. This principle ensures equal voting rights for all citizens and makes the country’s election process genuinely representative and fair.
The Election Commission of India guarantees transparent and efficient elections. Students should remember the importance of fair voting practices, like the secret ballot and accessibility measures, that empower every eligible voter in our diverse nation.
Regular practice of chapter-wise questions about elections in India will help you build a strong foundation for exams. Focus on the points that explain the significance of reserved seats, EVMs, and different types of elections for better clarity and scoring high marks.
FAQs on Class 8 Maths Chapter 5 Number Play – NCERT Stepwise Solutions
1. What are the key concepts covered in NCERT Solutions for Class 8 Maths Chapter 5 Number Play?
NCERT Solutions for Class 8 Maths Chapter 5 Number Play focus on important number properties, including divisibility tests, prime factorization, and patterns in numbers, all aligned with the latest CBSE syllabus. By working through stepwise solutions for each exercise, students build a strong foundation in concepts essential for exams.
2. How can I write stepwise answers for Class 8 Maths Chapter 5 Number Play to score full marks?
Presenting stepwise answers for Class 8 Maths Chapter 5 Number Play is crucial to scoring full marks in CBSE exams. Each step should be logical, clearly shown, and use correct terminology:
- Start with a brief statement of the question or given data
- Show each calculation or reasoning point separately
- Highlight formulas or definitions where used
- Draw boxes around final answers
- Follow the structure found in Vedantu’s NCERT Solutions for clarity and alignment with marking schemes
3. Which types of questions from NCERT Solutions Class 8 Maths Chapter 5 Number Play are frequently asked in CBSE exams?
NCERT Solutions for Class 8 Maths Chapter 5 Number Play often receive exam questions based on:
- Application of divisibility tests (especially 2, 3, 5, 9, 10)
- Identifying prime and composite numbers
- Expressing numbers as a product of primes
- Word problems involving factors and multiples
- Real-life situations requiring patterns or rules from the chapter
4. Are diagrams or definitions mandatory in answers for NCERT Solutions Class 8 Maths Chapter 5 Number Play?
Including accurate definitions is essential whenever the question asks for them, especially for terms like prime number, composite number, or divisibility. While diagrams are generally not required for this chapter, structured tables/boxes may sometimes help in presenting factors or stepwise methods more clearly, as demonstrated in Vedantu’s exercise-wise solutions.
5. Where can I download the free PDF of NCERT Solutions for Class 8 Maths Chapter 5 Number Play on Vedantu?
To access a free PDF of NCERT Solutions for Class 8 Maths Chapter 5 Number Play, simply use the download option provided by Vedantu on this chapter page. These PDFs are designed for offline revision, follow each exercise as per the textbook, and are updated for the CBSE 2025–26 syllabus.
6. What are the most important topics to focus on in NCERT Solutions for Class 8 Maths Chapter 5 Number Play for the CBSE 2025–26 exam?
Key topics from NCERT Solutions for Class 8 Maths Chapter 5 Number Play include:
- Divisibility rules and their applications
- Prime factorization techniques
- Identifying and writing multiples and factors
- Solving real-world application problems based on number properties
7. Do examiners award partial marks for correct steps even if the final answer is wrong in NCERT Solutions Class 8 Maths Chapter 5 Number Play?
Yes, for CBSE exams using NCERT Solutions for Class 8 Maths Chapter 5 Number Play, examiners generally award partial marks for each correctly shown calculation step, even if the final answer is incorrect. Ensure each step is clear and methodically written, as practiced in Vedantu’s solutions.
8. How do I structure long answers for Class 8 Maths Chapter 5 Number Play to impress CBSE examiners?
A well-structured long answer in Class 8 Maths Chapter 5 Number Play answers the question pointwise, uses clear headings for each part (like stepwise reasoning or explanations), and summarizes at the end. Practicing with Vedantu’s answer formats will help you align with expected standards.
9. Are NCERT Solutions enough for Class 8 Maths Chapter 5 Number Play, or should I use extra resources?
NCERT Solutions for Class 8 Maths Chapter 5 Number Play provided by Vedantu are usually sufficient to cover all core concepts and exam-style questions. However, for extra practice or higher-order thinking, you may attempt NCERT Exemplar and Vedantu-curated challenge problems to further boost your exam readiness.
10. What is the best way to revise NCERT Solutions for Class 8 Maths Chapter 5 Number Play before exams?
To revise NCERT Solutions for Class 8 Maths Chapter 5 Number Play quickly and effectively, follow Vedantu’s revision planner:
- Review all key definitions and formulae
- Practice at least one question from each exercise, focusing on stepwise logic
- Use Vedantu’s quick notes and flashcards for last-minute recall
- Attempt sample questions under timed conditions
11. How do I avoid common mistakes in exam answers for Class 8 Maths Chapter 5 Number Play?
Preventing errors when answering NCERT Solutions for Class 8 Maths Chapter 5 Number Play is important for success. Watch out for these common do’s and don’ts:
Do:- Show every calculation step
- Check divisibility rules carefully
- Circle final answers
- Skip definitions or explanations
- Mix up prime and composite numbers
- Write steps out of order
12. Are references to textbook page numbers helpful when revising NCERT Solutions for Class 8 Maths Chapter 5 Number Play?
Referring to textbook page numbers can help you quickly locate solutions for Class 8 Maths Chapter 5 Number Play in the NCERT book, ensuring no exercise or problem is missed. Vedantu’s solutions clearly indicate exercise numbers and topics, making revision smoother and faster for students preparing for CBSE exams.
