Understanding Sets, Relations, and Functions in Mathematics

Sets, relations, and functions are formal structures in mathematics used to classify objects, establish connections among elements, and describe rules associating elements of different collections.

Mathematical Definition and Description of Sets

Definition: A set is a well-defined collection of distinct objects, represented by listing its elements within curly brackets, for example, $A = \{1, 2, 3\}$, or by set-builder notation, such as $B = \{x \mid x \text{ is a prime } \leq 10\}$.

Cardinality of a set is denoted as $n(A)$ and represents the number of elements in set $A$.

The empty set (or null set) contains no elements, denoted as $\varnothing$ or $\{\}$.

A singleton set contains exactly one element.

• Finite and infinite sets
• Power set and its cardinality
• Universal and equal sets
• Subset and proper subset

If $A$ has $n$ elements, the power set $P(A)$ comprises all $2^{n}$ possible subsets of $A$.

Standard Set Operations and Algebraic Laws

Union ($A \cup B$), intersection ($A \cap B$), and difference ($A \setminus B$) are the primary operations on sets, with the universal set $U$ providing the context for complements $A' = U \setminus A$.

• Commutative, associative, distributive laws
• De Morgan's laws for complements
• Identity, null, and idempotent laws

De Morgan's laws state $(A \cup B)' = A' \cap B'$ and $(A \cap B)' = A' \cup B'$.

Structure of Ordered Pairs and Cartesian Products

An ordered pair $(a,b)$ consists of elements $a$ and $b$ from sets $A$ and $B$, where order matters, i.e., $(a,b) \neq (b,a)$ unless $a=b$.

The Cartesian product $A \times B$ is defined as the set $\{(a, b) \mid a \in A,\, b \in B\}$, which forms the foundation for defining relations and functions.

Definition and Classification of Mathematical Relations

Definition: Any subset $R$ of $A \times B$ is called a relation from $A$ to $B$; if $A = B$, $R$ is a relation on $A$.

• Domain and range of a relation
• Inverse and identity relations
• Empty, universal, and equivalence relations

Domain $D(R) = \{a \in A \mid \exists b \in B, (a,b) \in R\}$, and range $R(R) = \{b \in B \mid \exists a \in A, (a,b) \in R\}$.

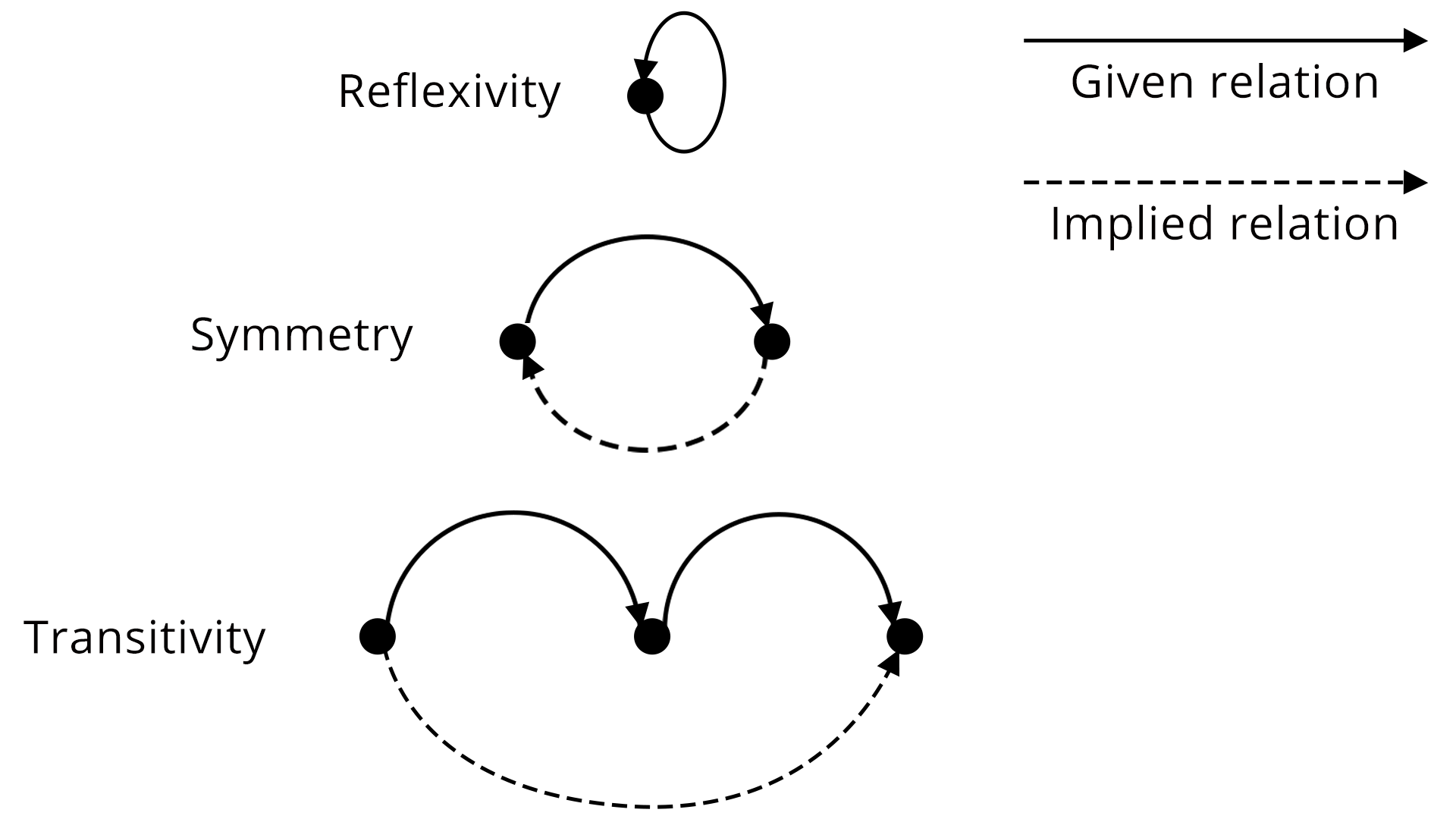
A relation is reflexive if $(a,a) \in R\, \forall a \in A$; symmetric if $(a,b)\in R \implies (b,a)\in R$; transitive if $(a,b)\in R$ and $(b,c)\in R \implies (a,c)\in R$. A relation is equivalence if it is reflexive, symmetric, and transitive.

For further relations question types, see Sets Relations And Functions Important Questions.

Mathematical Formulation of Functions and Mappings

Definition: A function $f$ from $A$ to $B$ (notation: $f : A \to B$) is a special relation where every $a \in A$ is associated with a unique $b \in B$, written $b = f(a)$.

• Domain, codomain, and range of a function
• Types: injective, surjective, bijective functions
• One-one, onto, many-one, into, constant functions

A function $f$ is injective if $f(a_{1}) = f(a_{2}) \implies a_{1} = a_{2}$ for all $a_{1}, a_{2} \in A$. It is surjective if for all $b \in B$, there exists $a \in A$ such that $f(a) = b$. It is bijective if both injective and surjective.

Constant functions map each element of $A$ to the same value in $B$. For in-depth functional forms, visit Functions And Its Types.

Principal Results Including Counting and Inclusion-Exclusion

Result: For two finite, possibly overlapping sets $A$ and $B$, the cardinality of their union is $n(A \cup B) = n(A) + n(B) - n(A \cap B)$. For three sets:

$n(A \cup B \cup C) = n(A) + n(B) + n(C) - n(A \cap B) - n(A \cap C) - n(B \cap C) + n(A \cap B \cap C)$

This counting principle is fundamental to problems in Permutations And Combinations and Probability.

• Inclusion-exclusion principle
• Number of subsets and possible relations
• Inverse of bijective functions
• Number of functions between finite sets

Worked Examples Based on Sets, Relations, and Functions

Example: Given $A = \{1, 2, 3\}$, $B = \{4, 5\}$, the Cartesian product $A \times B = \{(1,4), (1,5), (2,4), (2,5), (3,4), (3,5)\}$.

Direct substitution produces 3 elements in $A$, and 2 in $B$, so there are $3 \times 2 = 6$ ordered pairs.

Example: Let $R$ be the relation of divisibility from $A = \{3,5,7\}$ to $B = \{6,12,5,9\}$, i.e., $R = \{(a,b) | a \mid b\}$. By checking divisibility, $R = \{(3,6), (3,12), (3,9), (5,5)\}$.

Domain is $\{3,5\}$, codomain is $\{6,12,5,9\}$, and range is $\{6,12,5,9\}$.

Example: If $f(x) = \sin^{-1}x$, $g(x) = \frac{x^2-x-2}{2x^2-x-6}$, find domain of $f\circ g$. Solution: Solve $|g(x)| \leq 1$. This leads to $(x+1)^2 \leq (2x+3)^2$, or $3x^2 + 10x + 8 \geq 0$, i.e., $x \in (-\infty, -2] \cup \left[-\frac{4}{3}, \infty\right)$. Therefore, the domain is $(-\infty, -2] \cup \left[-\frac{4}{3}, \infty\right).$

For additional practice, consult Sets Relations And Functions Practice Paper.

Exam Cues and Typical Misconceptions

Exam Tip: When verifying if a relation is an equivalence relation, check all three properties (reflexivity, symmetry, transitivity) with full generality, not only for sample pairs.

A frequent error is confusing range and codomain: the range is always a subset of the codomain.

When evaluating the inverse of a function, ensure the original function is bijective; otherwise, an inverse does not exist as a function.

Always specify the reference universal set when discussing complements or operations involving complements.

For stepwise notes on all definitions and properties, refer to Sets Relations And Functions Revision Notes.