




How Does a Single Movable Pulley Make Work Easier?
A single movable pulley is a classic simple machine that transforms how we lift loads. It offers mechanical advantage, appearing in many real-life contexts and in concept-heavy Physics questions for competitive exams like JEE.
Basic Concepts of a Pulley System
A pulley consists of a grooved wheel with a rope, cable, or belt running along the groove. It is used to change the direction or magnitude of a force.
Pulleys enable us to lift heavy objects with less effort by redistributing weight and making lifting more efficient in mechanical systems.
When analyzing pulleys for examinations, assumptions like a massless, frictionless pulley and rope are often made. This simplifies calculation and focuses on fundamental principles.
Types of Pulley Systems
Pulleys are categorized by how they interact with the rope and the kind of support the wheel receives during operation.
- Fixed pulley: Only alters direction, no force advantage
- Movable pulley: Axis moves with load for force benefit
- Compound pulley: Both fixed and movable pulleys combined together
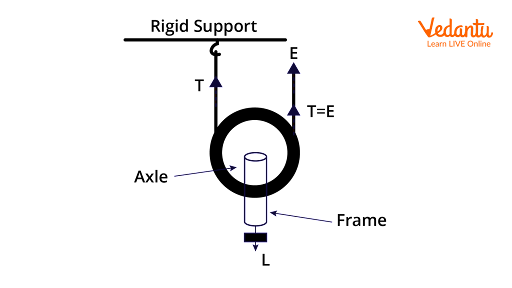
Defining the Single Movable Pulley Mechanism
A single movable pulley features a wheel whose axle is not fixed. The pulley moves along with the load, and one rope end is anchored.
When a person pulls on the free end of the rope, the movable pulley rises, bringing the load along. This setup effectively halves the effort needed compared to directly lifting.
A familiar analogy is the bucket in a well, where a movable pulley system makes pulling up water much easier than brute force alone.
Mechanical Advantage in Single Movable Pulleys
Mechanical advantage (MA) is a key term in pulley analysis. It is the ratio of load lifted ($L$) to effort applied ($E$).
For a single movable pulley without friction, the weight is supported by both rope segments. Thus, the tension on each supports half the total load.
The mechanical advantage in an ideal single movable pulley can be expressed as:
$MA = \dfrac{L}{E}$
When you pull down with force $E$, both segments of the rope attached to the moving pulley share the load equally.
$L = 2E$
$MA = \dfrac{L}{E} = \dfrac{2E}{E} = 2$
This means the effort required is halved, making lifting easier and more efficient in practical applications.
Velocity Ratio in a Single Movable Pulley
The velocity ratio (VR) is another important concept. It is the ratio of distance moved by the effort to distance moved by the load.
In an ideal single movable pulley, the velocity ratio also equals 2. Whenever the effort moves a certain distance, the load covers half that distance.
Class of Lever: Where Does It Fit?
A single movable pulley behaves like a class II lever. Here, the load is placed between the effort and the fulcrum, leading to a substantial advantage.
This links the pulley system to concepts in rotational dynamics and moments, helping build connections across Physics topics for exams like JEE.
Single Movable Versus Single Fixed Pulley
A fixed pulley only changes the direction of the applied force and does not offer mechanical advantage. The movable type reduces the effort required by distributing weight between rope segments.
| Feature | Single Movable Pulley |
|---|---|
| Mechanical Advantage | 2 |
| Velocity Ratio | 2 |
| Fixed or Movable Axis | Movable |
| Direction of Force Changed? | No |
Key Principles Linked to Pulleys
Understanding pulleys helps in studying energy transformations and mechanical efficiency in systems. This is crucial for chapters like Work, Energy, and Power.
Pulleys also help visualize force distribution, making them relevant when studying Torque and Rotational Motion.
When ropes stretch under load, the principles of Hooke's Law and Spring Force become significant. This connects static machines to elastic properties in Physics.
A moving pulley can accelerate, tying into kinematic analysis and the concept of Understanding Acceleration in Physics exams.
Oscillating or dynamic changes in a system with pulleys and springs may also link to Simple Harmonic Motion in advanced cases.
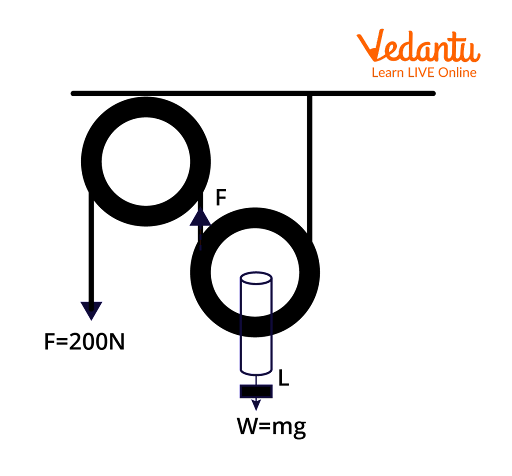
Illustrative Example: Solving a Single Movable Pulley Problem
Suppose you must lift a 40 kg block using an ideal single movable pulley. You want to know what effort ($E$) is needed.
Known: Mass $m = 40 \text{ kg}$, $g = 10\,\text{m/s}^2$, MA = 2.
Weight of load: $L = m \times g$
$L = 40 \times 10$
$L = 400\,\text{N}$
Formula: $MA = \dfrac{L}{E}$
Substitute: $2 = \dfrac{400}{E}$
$E = \dfrac{400}{2}$
Result: $E = 200\,\text{N}$. This means you only need to apply 200 N to lift a 40 kg mass.
Single Movable Pulley in Real Life
You can find single movable pulleys in construction cranes, elevators, and in rock-climbing equipment. These systems reliably reduce human effort in lifting loads.
- Used in hoisting machines for easier lifting
- Common in ropeways and rescue machines
- Helpful in gym equipment for controlled workouts
Common Mistakes in Pulley Problems
Pupils often forget to consider both rope segments supporting the load. This leads to incorrect effort calculations.
Ignoring the effect of friction or pulley mass in real-life scenarios can also give misleading results in answers.
It's important not to mix up velocity ratio and mechanical advantage; always check which to use in problems.
Practice Question for JEE Candidates
A 50 kg load is to be lifted using a single movable pulley. If the system is ideal, calculate the minimum effort needed.
Pulley Systems in Physics: Connecting with Bigger Ideas
Mastering pulleys builds a base for advanced mechanics. Understanding force splitting prepares you for torque, levers, and energy problems later in JEE Physics.
- Work, Energy, and Power
- Hooke's Law and Spring Force
- Torque and Rotational Motion
- Simple Harmonic Motion
- Acceleration Analysis
FAQs on Understanding Single Movable Pulleys: Easy Guide for Students
1. What is a single movable pulley?
A single movable pulley is a simple machine that helps lift a load with less effort by allowing the effort to move a greater distance than the load.
Key points:
- It consists of a grooved wheel that moves along with the load.
- The pulley is not fixed and moves up with the load as the effort is applied.
- It changes only the magnitude, not the direction, of the effort applied.
- This system is commonly used in construction and material handling.
2. What is the mechanical advantage of a single movable pulley?
The mechanical advantage of a single movable pulley is 2, assuming the pulley is ideal and frictionless.
This means:
- The effort required to lift a load is half of the load’s weight.
- Mechanical advantage (M.A.) = Load / Effort = 2 for an ideal single movable pulley.
3. How does a single movable pulley differ from a single fixed pulley?
A single movable pulley reduces the effort needed to lift a load, while a single fixed pulley only changes the direction of the force applied.
Main differences:
- Movable pulley: Provides mechanical advantage; effort is halved.
- Fixed pulley: No mechanical advantage; makes lifting more convenient.
4. State the principle on which a single movable pulley works.
A single movable pulley works on the principle of force multiplication, where the load is shared between the rope segments, reducing the effort needed to lift the object.
This means the input effort is distributed, making heavy loads easier to lift.
5. What is the velocity ratio of a single movable pulley?
The velocity ratio of a single movable pulley is 2.
This means:
- The effort moves twice the distance compared to the load.
- Velocity Ratio (V.R.) = Distance moved by effort / Distance moved by load = 2
6. What are the advantages and limitations of a single movable pulley?
Advantages:
- Reduces the effort needed to lift a load.
- Simple and easy to use for moderate loads.
- Cannot change the direction of the effort applied.
- Not suitable for very heavy loads unless combined with other pulleys.
- Friction and pulley weight reduce efficiency in real situations.
7. How do you calculate the efficiency of a single movable pulley?
Efficiency of a single movable pulley is calculated by comparing the work output to the work input.
Formula:
- Efficiency (%) = (Mechanical advantage / Velocity ratio) x 100
- For an ideal (frictionless) pulley, efficiency is 100%.
- In real cases, efficiency is always less than 100% due to friction and pulley mass.
8. Why is the mechanical advantage of a movable pulley less than 2 in real scenarios?
In real scenarios, the mechanical advantage is slightly less than 2 because of friction and the weight of the pulley itself.
Reasons include:
- Friction in the axle and rope reduces efficiency.
- The movable pulley has its own weight, adding to the effort needed.
9. What are some practical applications of single movable pulleys?
Single movable pulleys are widely used to lift heavy loads with less effort.
Examples include:
- Cranes at construction sites
- Elevators and hoists
- Rescue operations for lifting stretchers
- Window-cleaning platforms
10. What happens to the force required if the single movable pulley is not frictionless?
If a single movable pulley is not frictionless, more force is needed to lift the same load.
The presence of friction:
- Decreases the actual mechanical advantage
- Reduces efficiency
- Requires the user to apply more effort than in an ideal case
11. Why can a single movable pulley not be used as a force multiplier as effectively as a system of pulleys?
A single movable pulley provides limited mechanical advantage, usually up to 2, while a system of multiple pulleys (block and tackle) can multiply the force much more, making it more efficient for heavier loads.
12. What is the function of the rope in a single movable pulley?
The rope in a single movable pulley transmits the effort force to the load and supports the load's weight.
Functions:
- Divides the applied effort between the support and the load.
- Allows movement and lifting of the load upwards as the rope is pulled.

































