Class 10 Maths Chapter 11 Exercise 11.1 Areas Related to Circles NCERT Solutions

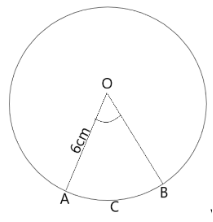
1. Find the area of a sector of a circle with radius 6 cm if the angle of the sector is \[{60^ \circ }\].$\pi =\dfrac{22}{7}$

Ans:

Given that, 

Radius of the circle = \[r = 6cm\]

Angle made by the sector with the center, \[\theta  = {60^ \circ }\]

Let OACB be a sector of the circle making \[{60^ \circ }\] angle at center O of the circle.

We know that area of sector of angle, \[ = \dfrac{\theta }{{{{360}^ \circ }}} \times \pi {r^2}\]

Thus, Area of sector OACB \[ = \dfrac{{{{60}^ \circ }}}{{{{360}^ \circ }}} \times \dfrac{{22}}{7} \times {(6)^2}\]

\[ = \dfrac{1}{6} \times \dfrac{{22}}{7} \times 6 \times 6\]

\[ = \dfrac{{132}}{7}c{m^2}\]

Therefore, the area of the sector of the circle making 60° at the center of the circle is \[\dfrac{{132}}{7}c{m^2}\].

2. Find the area of a quadrant of a circle whose circumference is 22 cm. $\text{Use } \pi =\dfrac{22}{7}$

Ans:

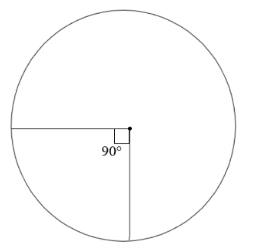
Given that,

Circumference = 22 cm

Let the radius of the circle be \[r\].

According to the given condition,

\[2\pi r = 22\]

\[ \Rightarrow r = \dfrac{{22}}{{2\pi }}\]

\[ = \dfrac{{11}}{\pi }\]

We know that, quadrant of a circle subtends \[{90^ \circ }\] angle at the center of the circle.

Area of such quadrant of the circle \[ = \dfrac{{{{90}^ \circ }}}{{{{360}^ \circ }}} \times \pi  \times {r^2}\]

\[ = \dfrac{1}{4} \times \pi  \times {\left( {\dfrac{{11}}{\pi }} \right)^2}\]

\[ = \dfrac{{121}}{{4\pi }}\]

\[ = \dfrac{{77}}{8}c{m^2}\]

Hence, the area of a quadrant of a circle whose circumference is 22 cm is \[ = \dfrac{{77}}{8}c{m^2}\].

3. The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.

$\text{Use } \pi =\dfrac{22}{7}$

Ans:

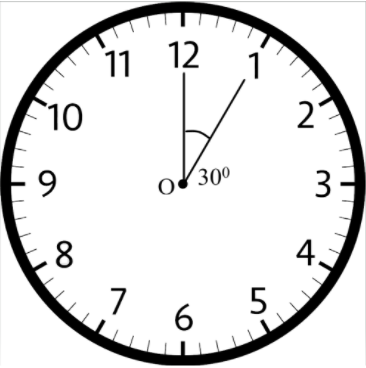
Given that,

Radius of clock or circle = \[r\] = 14 cm.

We know that in 1 hour (i.e., 60 minutes), the minute hand rotates \[{360^ \circ }\]. 

Thus, in 5 minutes, minute hand will rotate \[ = \dfrac{{{{360}^ \circ }}}{{{{60}^ \circ }}} \times 5\]

\[ = {30^ \circ }\]

Now, 

the area swept by the minute hand in 5 minutes = the area of a sector of \[{30^ \circ }\] in a circle of 14 cm radius.

 Area of sector of angle \[\theta  = \dfrac{\theta }{{{{360}^ \circ }}} \times \pi {r^2}\] 

 Thus, Area of sector of \[{30^ \circ } = \dfrac{{{{30}^ \circ }}}{{{{360}^ \circ }}} \times \dfrac{{22}}{7} \times 14 \times 14\]

\[ = \dfrac{{11 \times 14}}{3}\]

\[ = \dfrac{{154}}{3}c{m^2}\]

Therefore, the area swept by the minute hand in 5 minutes is \[\dfrac{{154}}{3}c{m^2}\].

4. A chord of a circle of radius 10 cm subtends a right angle at the center. Find the area of the corresponding:  $[\text{Use }\pi =3.14]$

Ans:

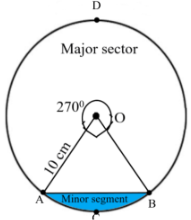
Given that, 

Radius of the circle \[ = r = 10cm\]

Angle subtended by the cord = angle for minor sector\[ = {90^ \circ }\]

Angle for major sector \[ = {360^ \circ } - {90^ \circ } = {270^ \circ }\]

(i) Minor segment 

Ans: It is evident from the figure that, 

Area of minor segment ACBA = Area of minor sector OACB − Area of ΔOAB

Thus,

Area of minor sector OACB \[ = \dfrac{{{{90}^ \circ }}}{{{{360}^ \circ }}} \times \pi {r^2}\] \[ = \dfrac{1}{4} \times 3.14 \times {(10)^2}\] \[ = 78.5c{m^2}\]

Area of ΔOAB \[ = \dfrac{1}{2} \times OA \times OB = \dfrac{1}{2} \times {(10)^2} = 50c{m^2}\]

Area of minor segment ACBA \[ = 78.5 - 50 = 28.5c{m^2}\]

Hence, area of minor segment is \[28.5c{m^2}\]

(ii) Major sector

Ans: It is evident from the figure that,

Area of major sector OADB \[ = \dfrac{{{{270}^ \circ }}}{{{{360}^ \circ }}} = \dfrac{3}{4} \times 3.14 \times {(10)^2} = 235.5c{m^2}\].

Hence, the area of the major sector is \[235.5c{m^2}\].

5. In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. 

$\pi =\dfrac{22}{7}$. Find: 

Ans:

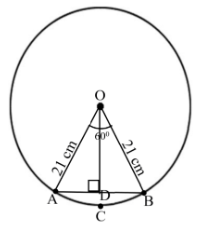
Given that, 

Radius of circle = \[r = \] 21 cm 

Angle subtended by the given arc = \[\theta  = {60^ \circ }\]

(i) The length of the arc

Ans: We know that, Length of an arc of a sector of angle \[\theta  = \dfrac{\theta }{{{{360}^ \circ }}} \times 2\pi r\]

Thus, Length of arc ACB \[ = \dfrac{{{{60}^ \circ }}}{{{{360}^ \circ }}} \times 2 \times \dfrac{{22}}{7} \times 21\]

\[ = 22cm\] 

Hence, the length of the arc of a given circle is \[22cm\].

(ii) Area of the sector formed by the arc 

Ans: We know that, Area of sector OACB \[ = \dfrac{{{{60}^ \circ }}}{{{{360}^ \circ }}} \times \pi {r^2}\]

\[ = 231c{m^2}\]

Hence, the area of the sector formed by the arc of the given circle is \[231c{m^2}\].

(iii) Area of the segment formed by the corresponding chord

Ans: In \[OAB\],

As radius \[OA = OB\]

\[ \Rightarrow \angle OAB = \angle OBA\]

\[\angle OAB + \angle AOB + \angle OBA = {180^ \circ }\]

\[2\angle OAB + {60^ \circ } = {180^ \circ }\]

\[\angle OAB = {60^ \circ }\]

Therefore, \[OAB\] is an equilateral triangle.

Now, area of \[OAB\] \[ = \dfrac{{\sqrt 3 }}{4} \times {\left( {side} \right)^2}\]

\[ = \dfrac{{\sqrt 3 }}{4} \times {\left( r \right)^2}\]

\[ = \dfrac{{\sqrt 3 }}{4} \times {\left( {21} \right)^2}\]

\[ = \dfrac{{441\sqrt 3 }}{4}c{m^2}\]

We know that, Area of segment ACB = Area of sector OACB − Area of $\Delta AOB$

\[ = \left( {231 - \dfrac{{441\sqrt 3 }}{4}} \right)c{m^2}\].

6. A chord of a circle of radius 15 cm subtends an angle of 60° at the center. Find the areas of the corresponding minor and major segments of the circle.

\[\text{Use}\pi =\dfrac{22}{7}, \sqrt{3}=1.73\]

Ans:

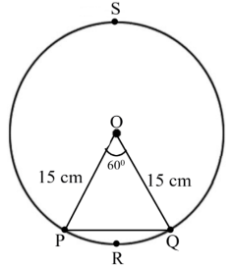
Given that, 

Radius of circle = \[r = \] 15 cm 

Angle subtended by chord \[ = \theta  = {60^ \circ }\]

Area of circle \[ = \pi {r^2}\] \[ = 3.14{\left( {15} \right)^2}\]

\[ = 706.5c{m^2}\]

Area of sector OPRQ \[ = \dfrac{{{{60}^ \circ }}}{{{{360}^ \circ }}} \times \pi {r^2}\]

 \[ = \dfrac{1}{6} \times 3.14{(15)^2} = 117.75c{m^2}\]

Now, for the area of major and minor segments, 

In \[OPQ\],

Since, \[OP = OQ\]

\[ \Rightarrow \angle OPQ = \angle OQP\]

\[\angle OPQ = {60^ \circ }\]

Thus, \[OPQ\] is an equilateral triangle.

Area of \[OPQ\] \[ = \dfrac{{\sqrt 3 }}{4} \times {\left( {side} \right)^2}\]

\[ = \dfrac{{\sqrt 3 }}{4} \times {(r)^2}\] 

\[ = \dfrac{{225\sqrt 3 }}{4}\] \[ = 97.3125c{m^2}\].

Now, 

Area of minor segment PRQP = Area of sector OPRQ − Area of \[OPQ\] 

\[ = 117.75 - 97.3125\]

\[ = 20.4375c{m^2}\]

Area of major segment PSQP = Area of circle − Area of minor segment PRQP 

\[ = 706.5 - 20.4375\]

\[ = 686.0625c{m^2}\]

Therefore, the areas of the corresponding minor and major segments of the circle are \[20.4375c{m^2}\] and \[686.0625c{m^2}\] respectively.

7. A chord of a circle of radius 12 cm subtends an angle of 120° at the center. Find the area of the corresponding segment of the circle. \[\text{Use}\pi =\dfrac{22}{7}\text{ and }\sqrt{3}=1.73\]

Ans: 

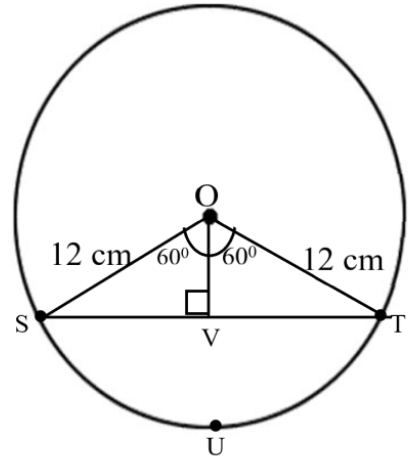
Draw a perpendicular OV on chord ST bisecting the chord ST such that SV = VT

Now, values of OV and ST are to be found.

Therefore, 

In \[OVS\],

\[\cos {60^ \circ } = \dfrac{{OV}}{{OS}}\]

\[ \Rightarrow \dfrac{{OV}}{{12}} = \dfrac{1}{2}\] 

\[ \Rightarrow OV = 6cm\]

Also, \[\dfrac{{SV}}{{SO}} = \sin {60^ \circ }\]

\[ \Rightarrow \dfrac{{SV}}{{12}} = \dfrac{{\sqrt 3 }}{2}\] 

\[ \Rightarrow SV = 6\sqrt 3 \]

Now, \[ST = 2SV\]

\[ = 2 \times 6\sqrt 3  = 12\sqrt 3 cm\]

Area of \[OST = \dfrac{1}{2} \times ST \times OV\]

\[ = \dfrac{1}{2} \times 12\sqrt 3  \times 6\]

\[ = 62.28c{m^2}\]

Area of sector OSUT \[ = \dfrac{{{{120}^ \circ }}}{{{{360}^ \circ }}} \times \pi {(12)^2}\]

 \[ = 150.42c{m^2}\]

Area of segment SUTS = Area of sector OSUT − Area of \[OVS\]

                                     \[ = 150.72 - 62.28\]

                                      \[ = 88.44c{m^2}\]

Hence, the area of the corresponding segment of the circle is \[88.44c{m^2}\].

8. A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see the given figure). \[\text{Use }\pi =3.14\]

Find 

Ans:

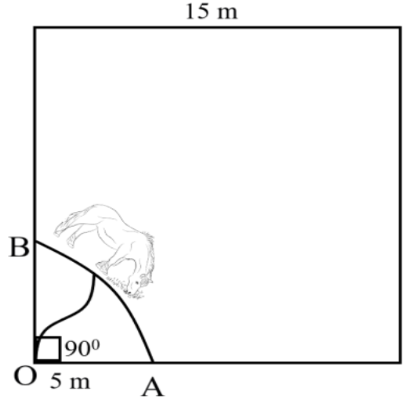
From the above figure, it is clear that the horse can graze a sector of \[{90^ \circ }\] in a circle of 5 m radius.

Hence, 

\[\theta \text{ }\!\!~\!\!\text{ }={{90}^{{}^\circ }}\]

\[r=5m\]

(i) The area of that part of the field in which the horse can graze.

Ans: It is evident from the figure,

Area that can be grazed by horse = Area of sector OACB

                                                       \[ = \dfrac{{{{90}^ \circ }}}{{{{360}^ \circ }}}\pi {r^2}\]

                                                        \[ = \dfrac{1}{4} \times 3.14 \times {(5)^2}\] \[ = 19.625{m^2}\]

(ii) The increase in the grazing area if the rope were 10 m long instead of 5 m.

Ans: It is evident from the figure,

Area that can be grazed by the horse when length of rope is 10 m long

\[ = \dfrac{{{{90}^ \circ }}}{{{{360}^ \circ }}} \times \pi  \times {(10)^2}\]

\[ = 78.5{m^2}\]

Therefore, the increase in grazing area for horse \[ = (78.5 - 19.625){m^2} = 58.875{m^2}\].

9. A brooch is made with silver wire in the form of a circle with a diameter 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in figure. $\pi =\dfrac{22}{7}$

Find:

Ans:

Given that, 

Radius of the circle \[ = r\] \[ = \dfrac{{diameter}}{2}\]\[ = \dfrac{{35}}{2}mm\]

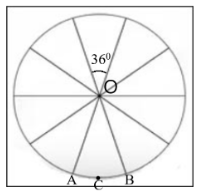
It can be observed from the figure that each of 10 sectors of the circle is subtending 36° (i.e., 360°/10=36°) at the center of the circle.

(i) The total length of the silver wire required.

Ans:

Total length of wire required will be the length of 5 diameters and the circumference of the brooch.

Circumference of brooch \[ = 2\pi r\]

                                         \[ = 2 \times \dfrac{{22}}{7} \times \left( {\dfrac{{35}}{2}} \right)\]

                                         \[ = 110mm\]

Length of wire required \[ = 110 + \left( {5 \times 35} \right)\]

                                        \[ = 285mm\]

Therefore, The total length of the silver wire required is \[285mm\].

(ii) The area of each sector of the brooch.

Ans:

Area of each sector \[ = \dfrac{{{{36}^ \circ }}}{{{{360}^ \circ }}} \times \pi {r^2}\]

                                 \[ = \dfrac{1}{{10}} \times \dfrac{{22}}{7} \times {\left( {\dfrac{{35}}{2}} \right)^2}\] 

                                 \[ = \dfrac{{385}}{4}m{m^2}\]

Hence, The area of each sector of the brooch is \[\dfrac{{385}}{4}m{m^2}\].

10. An umbrella has 8 ribs which are equally spaced (see figure). Assuming the umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella. $\pi =\dfrac{22}{7}$

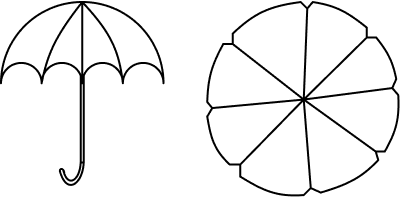
Ans: 

Given that, 

Radius of the umbrella \[ = r\]\[ = 45cm\]

There are 8 ribs in an umbrella. 

The angle between two consecutive ribs is subtending \[\dfrac{{{{360}^ \circ }}}{8} = {45^ \circ }\] at the center of the assumed flat circle. 

Area between two consecutive ribs of the assumed circle \[ = \dfrac{{{{45}^ \circ }}}{{{{360}^ \circ }}} \times \pi {r^2}\]

                                                                                            \[ = \dfrac{1}{8} \times \dfrac{{22}}{7} \times {\left( {45} \right)^2}\]

                                                                                            \[ = \dfrac{{22275}}{{28}}c{m^2}\] 

Hence, the area between the two consecutive ribs of the umbrella is \[\dfrac{{22275}}{{28}}c{m^2}\].

11. A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of ${115}^{\circ}$. Find the total area cleaned at \[{115^ \circ }\] each sweep of the blades. $\pi =\dfrac{22}{7}$

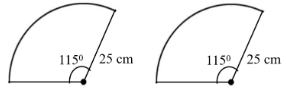
Ans:

Given that, 

Each blade of wiper will sweep an area of a sector of 115° in a circle of 25 cm radius.

Area of sector \[ = \dfrac{{{{115}^ \circ }}}{{{{360}^ \circ }}} \times \pi  \times {\left( {25} \right)^2}\]

                        \[ = \dfrac{{158125}}{{252}}c{m^2}\]

Area swept by 2 blades \[ = 2 \times \dfrac{{158125}}{{252}}\]

                                      \[ = \dfrac{{158125}}{{126}}c{m^2}\].

Therefore, the total area cleaned at each sweep of the blades is \[\dfrac{{158125}}{{126}}c{m^2}\].

12. To warn ships of underwater rocks, a lighthouse spreads a red colored light over a sector of angle \[{80^ \circ }\] to a distance of 16.5 km. Find the area of the sea over which the ships warned. \[\text{Use}\text{ }\pi =3.14\]

Ans: 

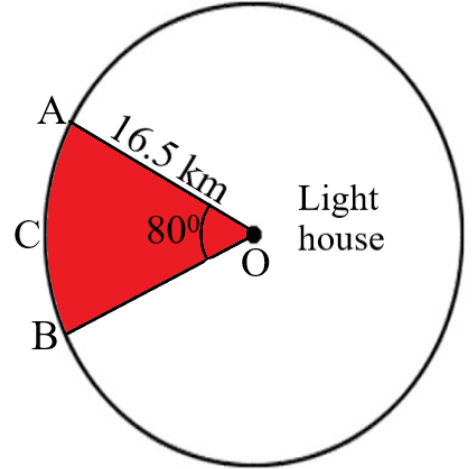
Given that, 

The lighthouse spreads light across a sector (represented by the shaded part in the figure) of \[{80^ \circ }\] in a circle of 16.5 km radius. 

Area of sector OACB \[ = \dfrac{{{{80}^ \circ }}}{{{{360}^ \circ }}} \times \pi {r^2}\]

                                    \[ = \dfrac{2}{9} \times 3.14 \times {(16.5)^2}\]

                                    \[ = 189.97k{m^2}\]

Hence, the area of the sea over which the ships are warned is \[189.97k{m^2}\].

13. A round table cover has six equal designs as shown in figure. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs.0.35 per ${cm}^{2}$.\[\text{Use}\sqrt{3}=1.7\text{ }\]

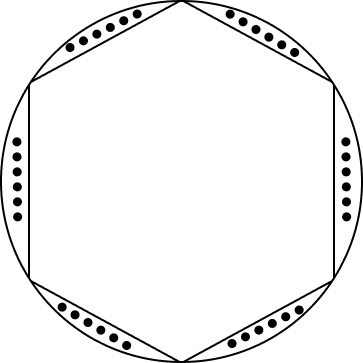
Ans:

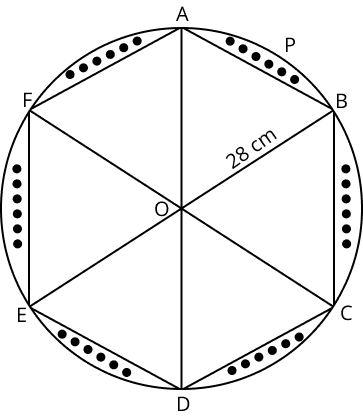
Given in the figure,

The designs are segments of the circle. 

Radius of the circle is 28cm.

Consider segment APB and chord AB is a side of the hexagon. 

Each chord will substitute at \[\dfrac{{{{360}^ \circ }}}{6} = {60^ \circ }\] at the center of the circle.

In \[OAB\],

Since, \[OA = OB\]

\[ \Rightarrow \angle OAB + \angle OBA + \angle AOB = {180^ \circ }\]

\[2\angle OAB = {180^ \circ } - {60^ \circ } = {120^ \circ }\]

\[\angle OAB = {60^ \circ }\]

Therefore, \[OAB\] is an equilateral triangle. 

Area of \[OAB\] \[ = \dfrac{{\sqrt 3 }}{4} \times {\left( {side} \right)^2}\]

                        \[ = \dfrac{{\sqrt 3 }}{4} \times {\left( {28} \right)^2}\]

                        \[ = 333.2c{m^2}\]

Area of sector OAPB \[ = \dfrac{{{{60}^ \circ }}}{{{{360}^ \circ }}} \times \pi {r^2}\]

                                   \[ = \dfrac{1}{6} \times \dfrac{{22}}{7} \times {(28)^2}\]

                                   \[ = \dfrac{{1232}}{3}c{m^2}\] 

Area of segment APBA = Area of sector OAPB − Area of ∆OAB

                                       \[ = \left( {\dfrac{{1232}}{3} - 333.2} \right)c{m^2}\]

Therefore, area of designs \[ = 6 \times \left( {\dfrac{{1232}}{3} - 333.2} \right)c{m^2}\]

                                           \[ = 464.8c{m^2}\]

Now, given that Cost of making 1 \[c{m^2}\] designs = Rs 0.35 

Cost of making 464.76 \[c{m^2}\] designs \[ = 464.8 \times 0.35 = \]162.68 

Therefore, the cost of making such designs is Rs 162.68.

14. Tick the correct answer in the following: Area of a sector of angle \[p\] (in degrees) of a circle with radius \[R\] is \[(A)\dfrac{P}{{180}} \times 2\pi R\] \[(B)\dfrac{P}{{180}} \times 2\pi {R^2}\] \[(C)\dfrac{P}{{180}} \times \pi R\] \[(D)\dfrac{P}{{720}} \times 2\pi {R^2}\]

Ans: 

We know that area of sector of angle \[\theta  = \dfrac{\theta }{{{{360}^ \circ }}} \times \pi {R^2}\] 

So, Area of sector of angle \[P = \dfrac{P}{{{{360}^ \circ }}}\left( {\pi {R^2}} \right)\] 

                                                \[ = \left( {\dfrac{P}{{{{720}^ \circ }}}} \right)\left( {2\pi {R^2}} \right)\]

Hence, (D) is the correct answer.

Conclusion

Class 10 Maths Chapter 11.1, "Areas Related to Circles," provides a solid foundation for understanding and calculating the areas of circles, sectors, and segments. By mastering these calculations, students gain essential skills that are applicable in both academic and real-world scenarios. Ex 11.1 Class 10 emphasizes the importance of precise formula application and enhances problem-solving abilities. Completing these problems will not only prepare students for exams but also build confidence in handling geometric concepts, paving the way for advanced studies in mathematics.

CBSE Class 10 Maths Chapter 11 Other Study Materials

Chapter-Specific NCERT Solutions for Class 10 Maths

Given below are the chapter-wise NCERT Solutions for Class 10 Maths. Go through these chapter-wise solutions to be thoroughly familiar with the concepts.

Study Resources for Class 10 Maths

For complete preparation of Maths for CBSE Class 10 board exams, check out the following links for different study materials available at Vedantu.