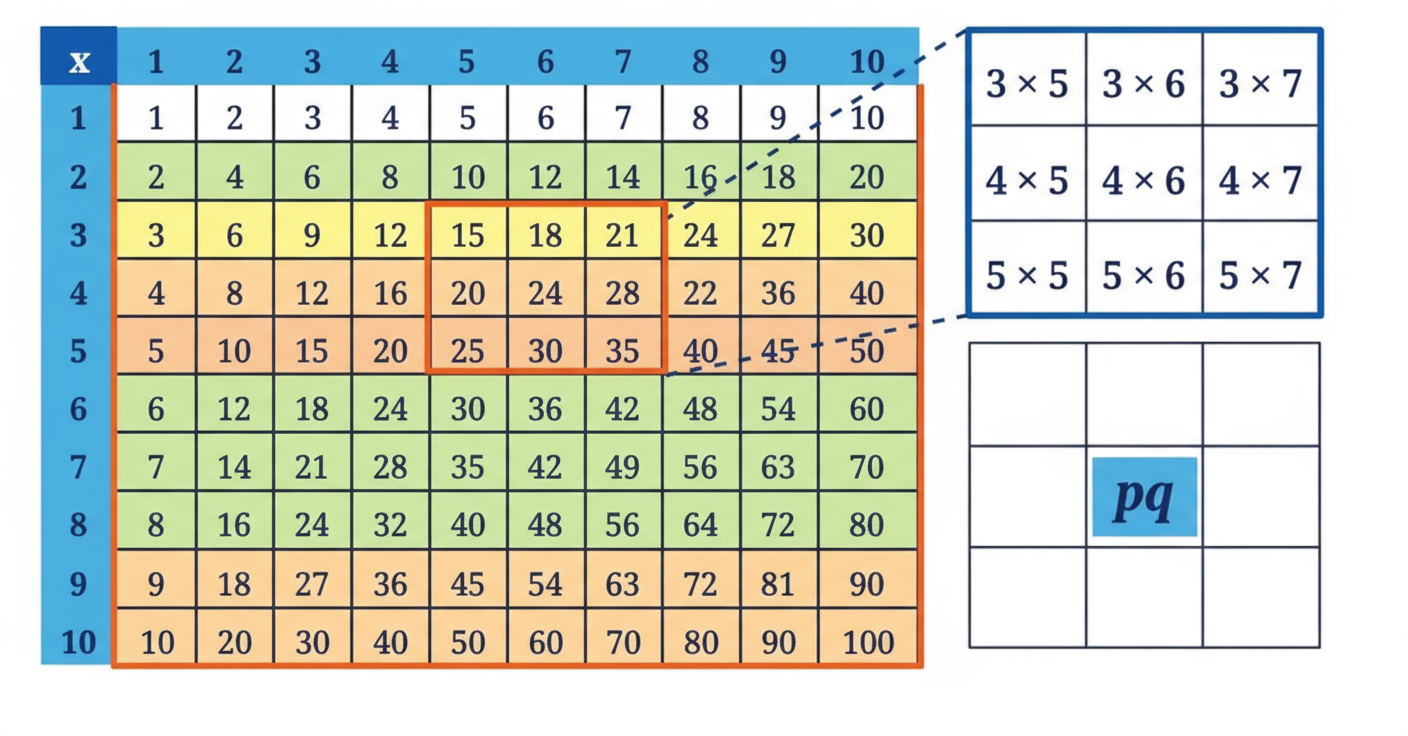
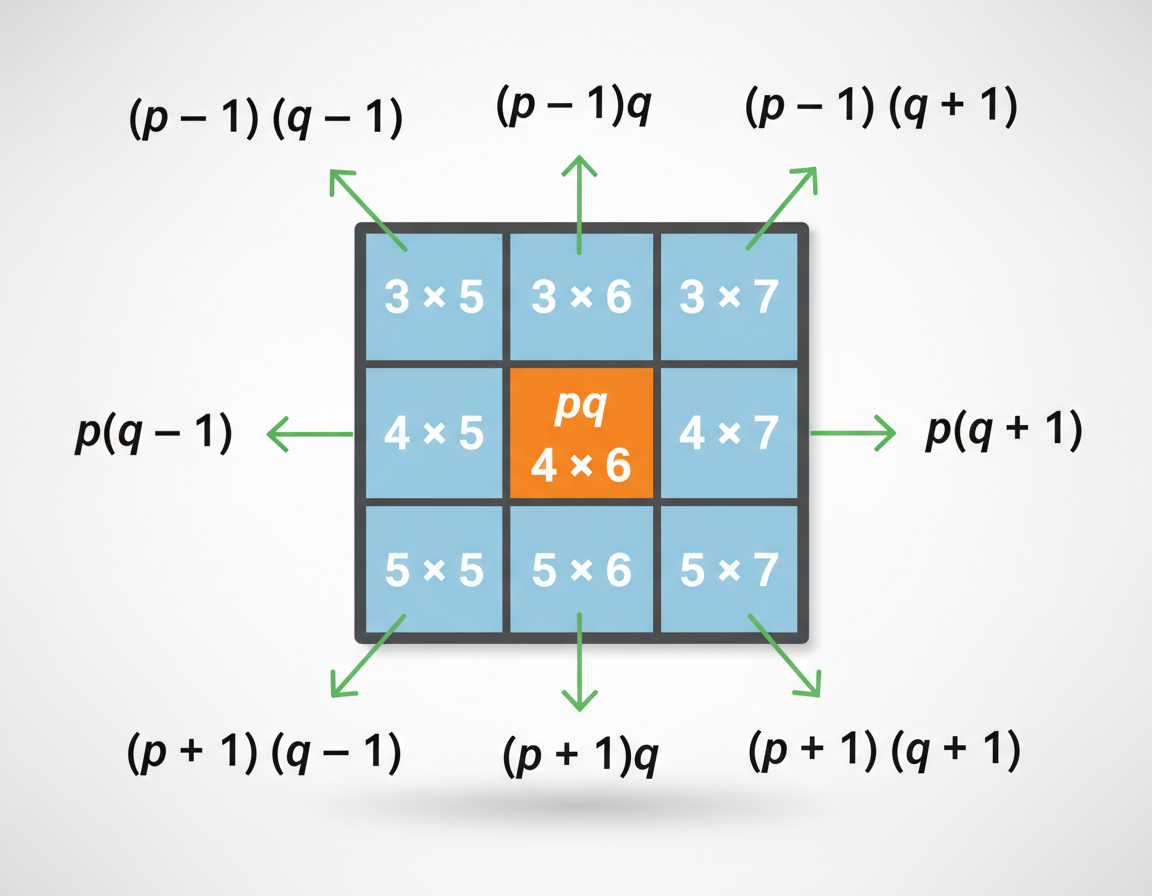
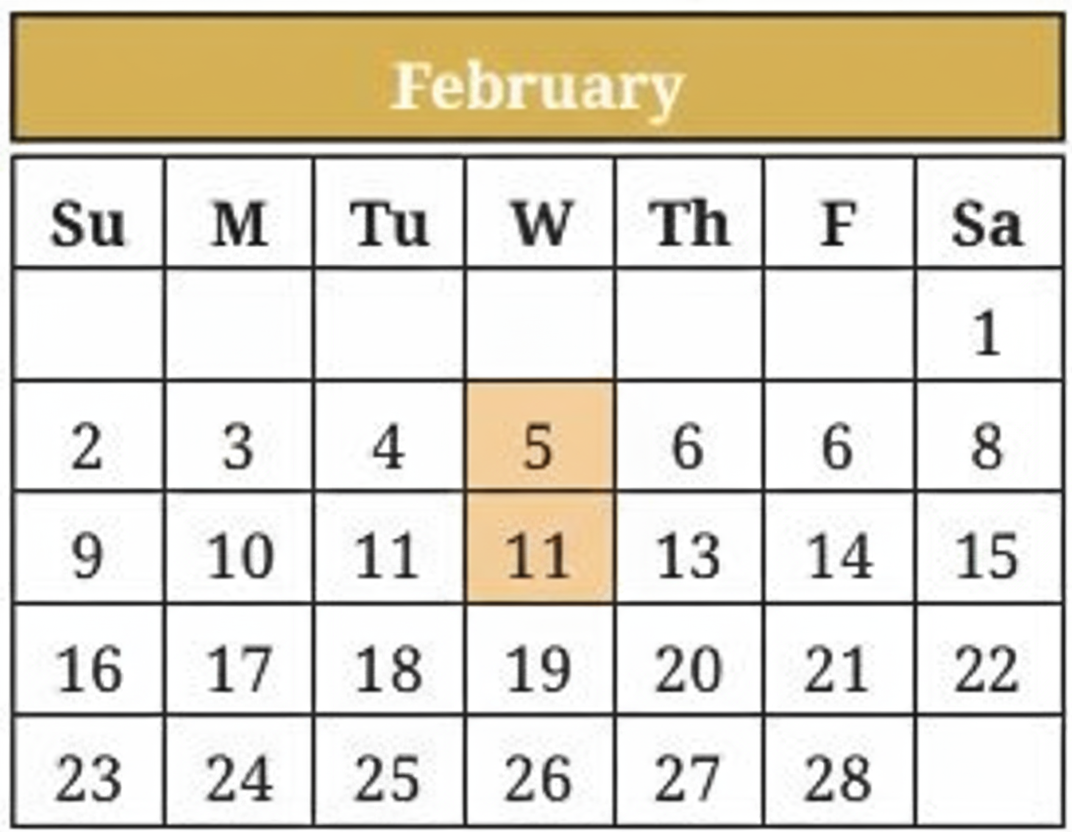
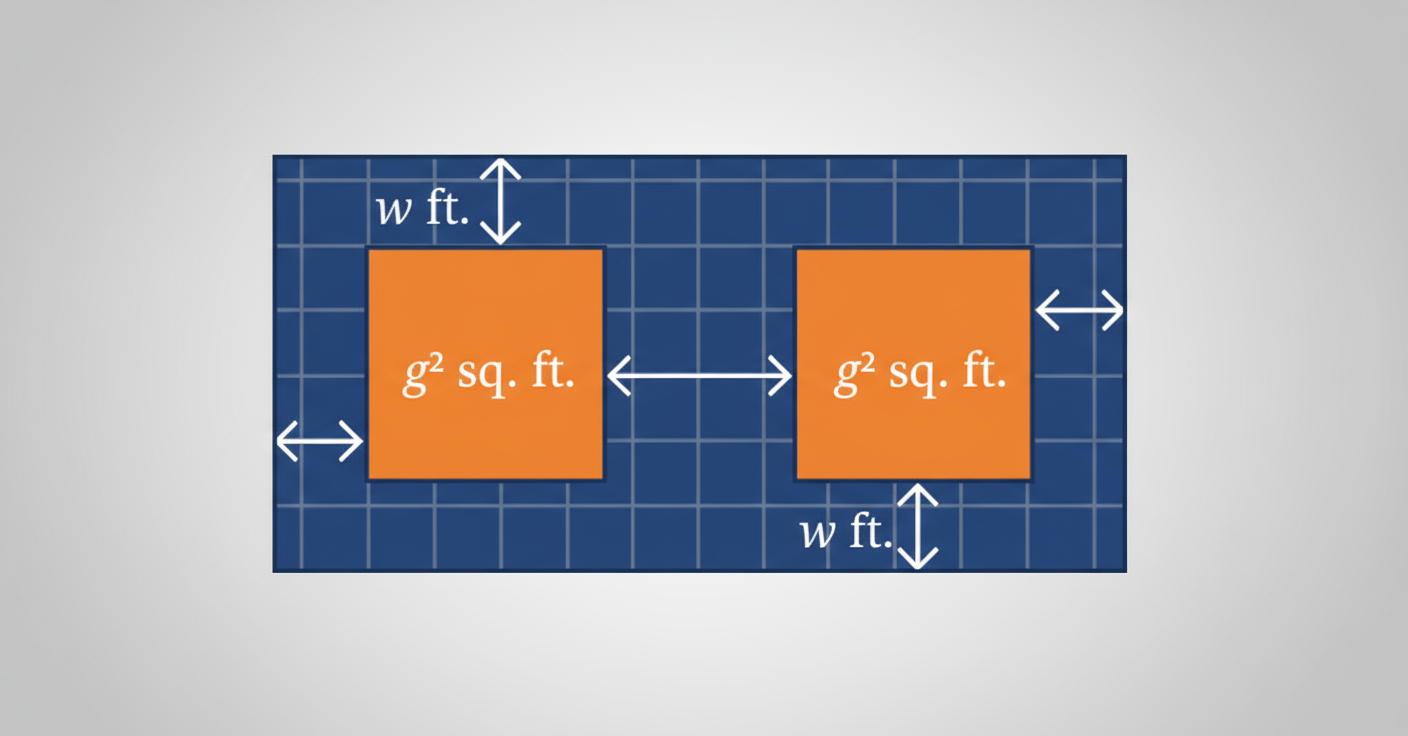
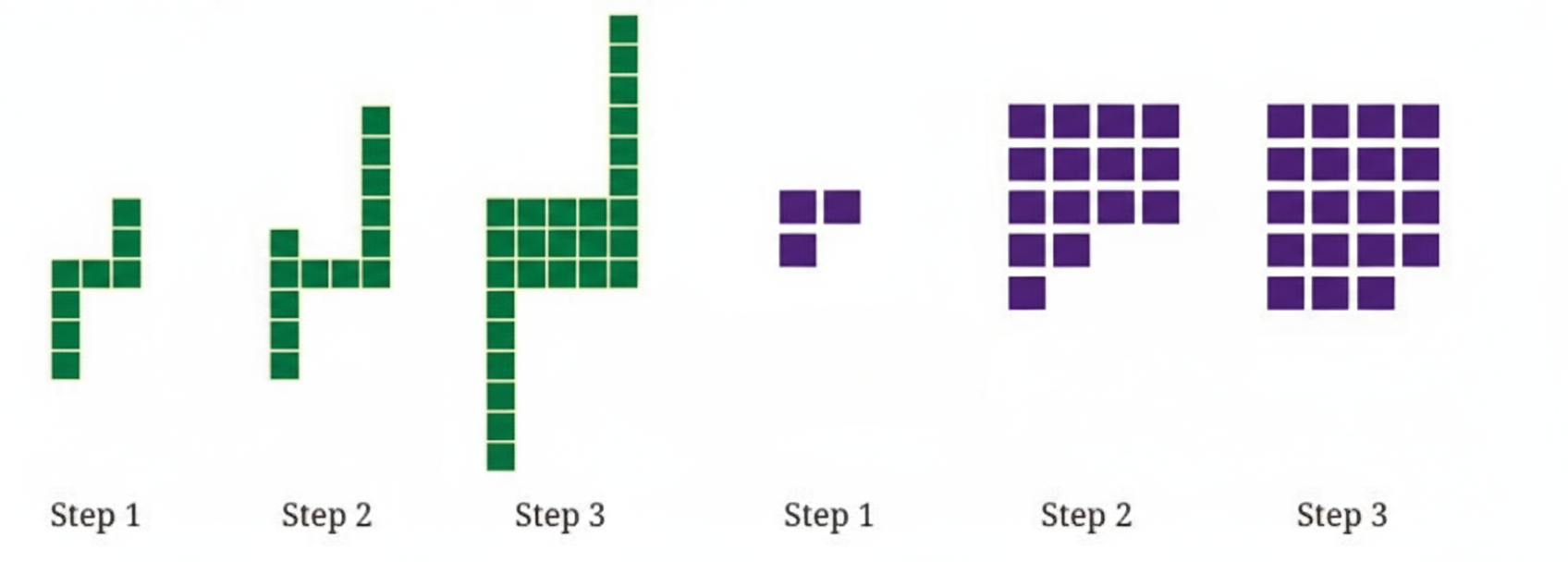
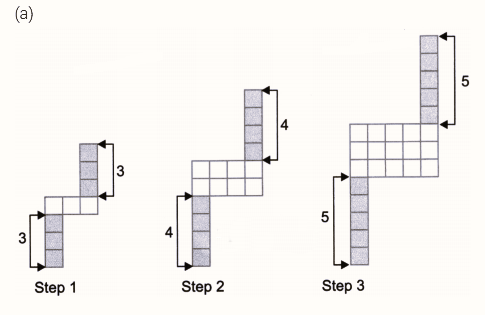
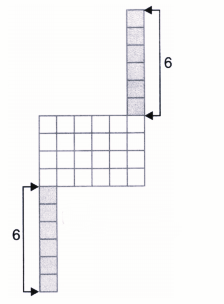
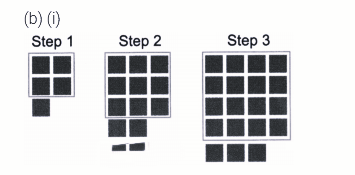
Exercise-wise NCERT Solutions for Class 8 Maths Chapter 6 with Marking Scheme
FAQs on NCERT Solutions For Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply (2025-26)
1. What is covered in the NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply?
NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply provided by Vedantu include stepwise answers to all textbook exercises, helping students master distributive properties and multiplication strategies. These solutions are essential for understanding key concepts, preparing for CBSE 2025–26 exams, and supporting quick revisions with concise notes and marking scheme insights.
2. How can I use the NCERT Solutions for Class 8 Maths Chapter 6 to score full marks in CBSE exams?
To score full marks, study NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply from Vedantu by following a strategic approach:
- Understand and practice each stepwise answer for every exercise.
- Use exam-oriented tips and highlight important keywords in your answers.
- Revise all key definitions and formulae provided in the chapter solutions.
- Analyze common mistakes shared in the solution guide to avoid errors.
3. Are diagrams or definitions mandatory in answers for NCERT Solutions Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply?
Including relevant diagrams and well-written definitions in your answers for NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply often earns additional marks. CBSE marking schemes encourage neat diagrams where applicable and accurate definitions for terms explained in the chapter. Always check the exercise for such requirements to maximize your scores.
4. Where can I download the free PDF of NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply?
You can easily download the free PDF of NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply directly from Vedantu. This resource allows CBSE 2025–26 students to study offline, revise concepts quickly, and prepare more effectively for school exams with reliable, exercise-wise solutions.
5. How should I present long answers in the NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply as per CBSE marking?
Presenting long answers effectively using NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply is crucial for securing full CBSE marks:
- Begin with a clear introduction referencing the key concept.
- Break down each calculation into neat, numbered steps.
- Highlight important keywords and formulas as per the marking scheme.
- Conclude with the final answer and units where needed.
6. What are the most important topics and questions from NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply?
Critical topics in NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply cover distributive properties, multiplication of algebraic expressions, and application-based problems. Pay extra attention to exercises involving formula application, solved exemplars, and CBSE exam pattern questions, as these are frequently tested in school assessments.
7. What key definitions and formulae should I revise from Class 8 Maths Chapter 6 NCERT Solutions?
Revising key definitions and formulae is essential for Class 8 CBSE exams. In NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply, focus on the following:
- Definition of distributive property
- Multiplication rules for algebraic terms
- Identifying like and unlike terms
- Standard short formulas for quick calculations
8. Do examiners award partial marks for correct steps even if the final answer is wrong in NCERT Solutions Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply?
Yes, CBSE examiners often award partial marks for correct stepwise working in answers from NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply, even if the final answer is incorrect. Therefore, always show all calculation steps and logical reasoning to maximize your score, as per the CBSE marking scheme.
9. How do I avoid common mistakes when using NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply?
Being careful when practicing with NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply helps you prevent frequent errors:
- Read each question carefully to understand what is asked.
- Write each calculation and simplification step.
- Double-check signs plus minus, and multiplication rules.
- Revise key concepts and avoid skipping definitions or diagrams.
- Practice CBSE exam-style questions from Vedantu to build confidence.
10. Are references to textbook page numbers helpful during revision of NCERT Solutions Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply?
Referencing textbook page numbers alongside NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply can be very useful during revision, as it helps you locate specific examples and explanations quickly. Vedantu often provides this mapping, making your last-minute preparation faster and more organized.
11. What is the best way to revise NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply before exams?
Revision is most effective when you plan it well with NCERT Solutions for Class 8 Maths Chapter 6 We Distribute, Yet Things Multiply: start with a 1-day overview of all exercises, spend 3 days focusing on tricky problems, and use Vedantu's flash notes for rapid recall. For in-depth prep, consistently review summarised key formulae and attempt sample questions to solidify your understanding.