Question

The area of square inscribed in a circle of diameter ‘p’cm is-
A. ${P^2}$ cm sq
B. $\dfrac{p}{4}$ cm sq
C. $\dfrac{{{p^2}}}{2}$ cm sq
D. $\dfrac{p}{2}$ cm sq

Answer 1

Hint: First we draw a square inscribed in a circle, then form a diameter in the square of ‘p’ cm then by using Pythagoras theorem calculate any side of the square. And finally find the area of square to get the final answer by using the formula : Area of square = ${\left( {{\text{side}}} \right)^2}$

Formula: Pythagoras Theorem
$A{B^2} + B{C^2} = A{C^2}$
And area of square = ${\left( {{\text{side}}} \right)^2}$

Complete step-by-step solution
Consider the diagram of the square inscribed circle with diameter of p cm.



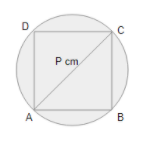
Given that the diameter of the circle is p cm. so the diagonal of the square is also p cm
Now by using the formula of Pythagoras theorem
Pythagoras theorem- A theorem attributed to the Pythagoras that the square on the hypotenuse of a right angled triangle is equal to the sum of squares on the other two sides.
$
  A{B^2} + B{C^2} + A{C^2} \\
  A{B^2} + A{B^2} = {P^2} \\
   \Rightarrow 2A{B^2} = {P^2} \\
   \Rightarrow AB = \dfrac{P}{{\sqrt 2 }} \\
 $
Now the area of square is
Area= square of side
\[
   \Rightarrow \dfrac{p}{{\sqrt 2 }} \times \dfrac{p}{{\sqrt 2 }} \\
   \Rightarrow \dfrac{{{p^2}}}{2} \\
 \]
So the area is $\dfrac{{{p^2}}}{2}{\text{cm sq}}$
Hence option C is the correct answer.

Note- First we draw a diagram according to the question and draw a diameter in it of P cm, after that using Pythagoras theorem find the side of square and then from this find the area of square and answer is $\dfrac{{{p^2}}}{2}{\text{cm sq}}$.