
The centroid of a triangle is the point of concurrence of its:
A. Angle bisectors
B. Perpendicular bisectors
C. Altitudes
D. Medians
Answer
204.6k+ views
Hint: First of all find the meaning of angle bisectors, perpendicular bisectors, altitudes and medians. Apply the definitions of centroid, orthocenter, circumcenter and incenter of a triangle. From the definition of centroid, it is the point where all the medians of a triangle intersects.
Complete step by step answer
As we know, angle bisectors are lines that divide the angle of a triangle in two equal parts such as in the figure below, line $AD$ is dividing $\angle A$ in two parts.
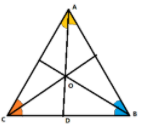
The point where all the angle bisectors of the triangle meet is known as the incenter of the triangle.
Perpendicular bisector from a vertex divide the opposite side in two equal parts and makes an angle of ${90^ \circ }$
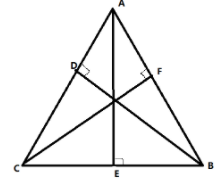
In the above figure, $AE \bot BC$ and $CE = EB$, therefore, $AE$ is a perpendicular bisector.
The point where perpendicular bisectors meet is known as the circumcenter of the triangle.
Altitude from a vertex makes an angle of ${90^ \circ }$ on the opposite side.
For example, the line $AE$ which makes a right angle from vertex $A$ on line $BC$, hence $AE$ is an altitude.
The point where the altitudes meet in a triangle is known as the orthocenter.
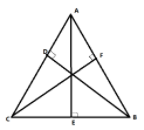
Medians are the lines that bisect the sides of the triangle.
The line $AE$ divides line $BC$ into equal parts, hence is the median.
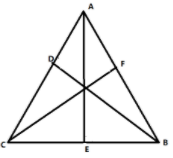
When medians meet at a point, it is known as the centroid.
Therefore, the centroid of a triangle is the point of concurrence of its medians.
Hence, option D is correct.
Note: Median bisects the opposite side and not the angle from which it is drawn. The lines that divide the angle of a triangle in two equal parts are angle bisectors. In a triangle, the centroid divides the median in 2:1 from the vertex the median is drawn. The centroid of a triangle always lies inside the triangle.
Complete step by step answer
As we know, angle bisectors are lines that divide the angle of a triangle in two equal parts such as in the figure below, line $AD$ is dividing $\angle A$ in two parts.

The point where all the angle bisectors of the triangle meet is known as the incenter of the triangle.
Perpendicular bisector from a vertex divide the opposite side in two equal parts and makes an angle of ${90^ \circ }$

In the above figure, $AE \bot BC$ and $CE = EB$, therefore, $AE$ is a perpendicular bisector.
The point where perpendicular bisectors meet is known as the circumcenter of the triangle.
Altitude from a vertex makes an angle of ${90^ \circ }$ on the opposite side.

For example, the line $AE$ which makes a right angle from vertex $A$ on line $BC$, hence $AE$ is an altitude.
The point where the altitudes meet in a triangle is known as the orthocenter.
Medians are the lines that bisect the sides of the triangle.

The line $AE$ divides line $BC$ into equal parts, hence is the median.
When medians meet at a point, it is known as the centroid.
Therefore, the centroid of a triangle is the point of concurrence of its medians.
Hence, option D is correct.
Note: Median bisects the opposite side and not the angle from which it is drawn. The lines that divide the angle of a triangle in two equal parts are angle bisectors. In a triangle, the centroid divides the median in 2:1 from the vertex the median is drawn. The centroid of a triangle always lies inside the triangle.
Recently Updated Pages
If 81 is the discriminant of 2x2 + 5x k 0 then the class 10 maths JEE_Main

The weight of a 13 m long iron rod is 234 kg The weight class 10 maths JEE_Main

The centroid of a triangle is the point of concurrence class 10 maths JEE_Main

A man on tour travels first 160 km at 64 kmhr and -class-10-maths-JEE_Main

The population of a city increases each year by 4 of class 10 maths JEE_Main

The area of square inscribed in a circle of diameter class 10 maths JEE_Main

Trending doubts
JEE Main 2026: Exam Date, Syllabus, Eligibility, Application Form & Preparation Tips

NTA JEE Main 2026 Registration Live: Check Dates, Fees, and Eligibility Here

JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main Syllabus 2026 (Updated)

Newton’s Laws of Motion Explained: Concepts, Formulas & Uses

JEE Main 2026 Syllabus PDF - Download Paper 1 and 2 Syllabus by NTA

Other Pages
NCERT Solutions For Class 10 Maths Chapter 12 Surface Area And Volume

NCERT Solutions for Class 10 Maths Chapter Chapter 13 Statistics

NCERT Solutions for Class 10 Maths Chapter 11 Areas Related to Circles 2025-26

NCERT Solutions for Class 10 Maths Chapter 15 Probability

Pregnancy Week and Due Date Calculator: Find How Far Along You Are

All Mensuration Formulas with Examples and Quick Revision




