




How to Calculate Area of Common 2D Shapes Efficiently
In Geometry, a shape is defined as a figure that is enclosed by a boundary. The border of the shapes is formed by lines, points, and curves. Two-dimensional (2D) shapes are bordered by straight lines. The 2D shapes have only length and breadth and they are popularly known as polygons and flat shapes. These include squares, rectangles, circles, rhombuses, and triangles. The area of a 2D shape is the region enclosed within the boundary which is measured in square units. Now, we will discuss more details about basic 2-dimensional shapes and their Areas.
Area of a Rectangle
The area of a rectangle in a two-dimensional region is the area covered by the rectangle. A rectangle is a two-dimensional form with four sides and four vertices. All the four angles in a rectangle are 90 degrees. The opposite sides of the rectangle are equal and parallel to one another.
Formula: Area of a rectangle = Length (L) x Breadth (W) (or width)
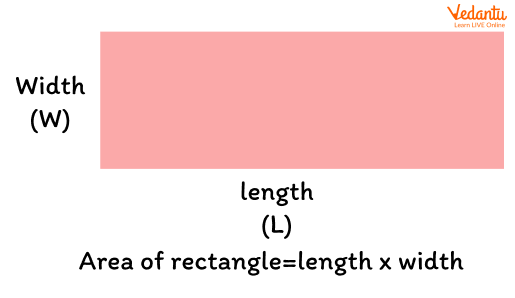
The shaded region represents the area of a rectangle with length and width
Example: Find the area of a rectangle with a length of 4 metres and a width of 2 metres.
Ans: Given length L = 4 m and width (W) = 2m
Area of the given rectangle = 4 x 2 = 8 sq.m
Area of a Square
A Square is a 2-Dimensional shape just like a rectangle. The only difference between a square and a rectangle is that in a rectangle only opposite sides are equal whereas in a square shape, all sides are equal. We can say a square is a rectangle with all of its sides being the same length.
Formula: Area of a square = side x side = (side)2
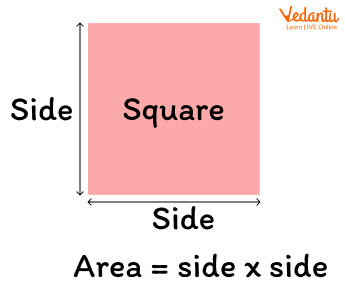
The shaded region represents the area of a square
Example: Find the area of a square whose side measures 3 cm.
Ans: Given the side of a square = 3cm
So, the area of the square = 3 x 3 = 9 sq.cm.
Area of a Circle
A circle is a closed curve with an exterior line that is equidistant from the centre. The radius of the circle is the fixed distance from the centre point to the boundary of the circle. Many examples of the circle can be found in everyday life, such as a wheel, pizzas, a round ground, and so on.
Formula: Area of circle with radius ‘r’ is given by the formula A = πr2
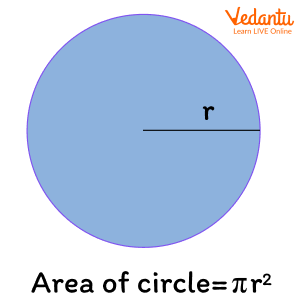
Shaded region represents the area of a circle with radius r.
Example: Find the area of a circle whose radius is 5 metres.
Ans: Given, radius of the circle r = 5m
Therefore, area of the circle = π(5)2= π(25) = 25 square units
Area of a Triangle
A triangle is one of the most fundamental 2-Dimensional shapes with three sides and three vertices. The area of the triangle is the region occupied inside the boundary of the triangle.
Formula: Area of a triangle with base ‘b’ and height ‘h’ = 1/2 base x height
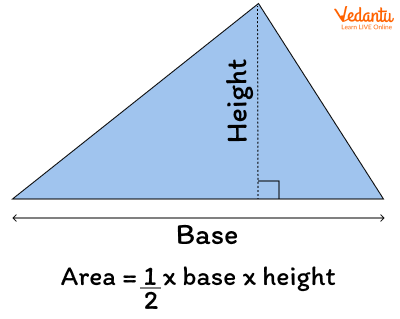
The shaded region represents the area of a triangle with base (b) and height (h).
Example: Find the area of the triangle with height 4m and base 3m.
Ans: Given, the height of the triangle (h) = 4m
The base of the triangle (b) = 3m
Area of the triangle = $\frac{1}{2}$ x 4 x 3 = 6 sq.m
Area of an Equilateral Triangle
An equilateral triangle is a type of triangle in which all sides are equal in length.
Formula: Area of an equilateral triangle = $\frac{\sqrt{3}}{4}$ x side2
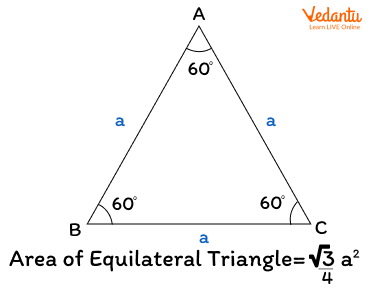
The shaded region in the above image shows the area of an equilateral triangle with side ‘a’.
Example: Find the area of an equilateral triangle with side length equal to 2m.
Ans: Given the side of an equilateral triangle is 2m.
So, the area of the given equilateral triangle is = $\frac{\sqrt{3}}{4}$ x (2)2 = $\sqrt{3}$ sq. m
Area of a Parallelogram
A parallelogram is a quadrilateral, in which opposite sides are equal in length and parallel but the angles are not equal to 90 degrees.
Formula: The area of a parallelogram with base ‘b’ and height ‘h’ is
A = base (b) x height (h)
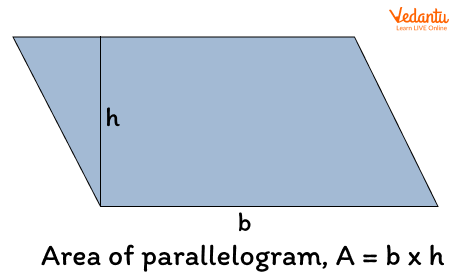
The shaded region shows the area of a parallelogram
Example: Find the area of a parallelogram with a base length of 9m and height of 3m.
Ans: Given, parallelogram has base length b = 9m and height h = 3m.
So, the area of the given parallelogram is A = 3 x 9 = 27 sq.m
Areas of 2D Shapes Chart
The below chart shows various two-dimensional shapes with their corresponding formulas which can be kept handy to refer to in future.
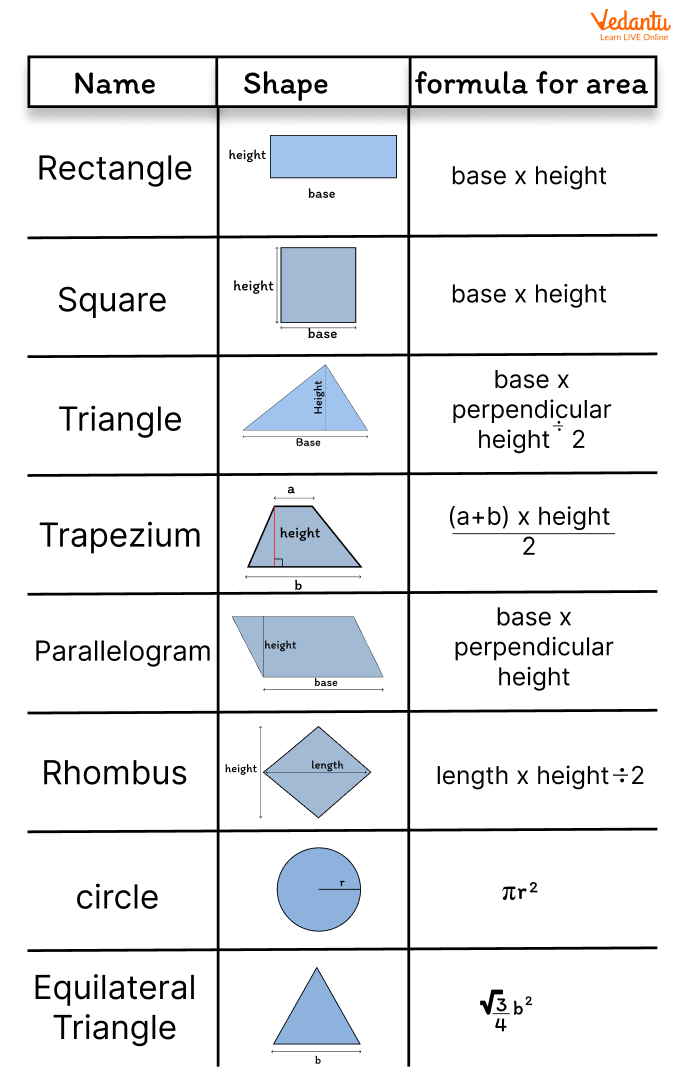
The above table shows 2D shapes and their corresponding areas.
Conclusion
In Mathematics, 2D shapes are planar figures that can be drawn on a flat surface or a sheet of paper. Two-dimensional shapes have sides and corners, while others have curved boundaries. The area of a 2-D shape is the region enclosed within the boundary of the shape. Learning 2D shapes and their areas is fun and helps the kids to improve their geometry skills.
FAQs on Area of 2D Shapes: Definitions, Formulas & Real-Life Examples
1. How do you find the area of a two-dimensional shape?
To find the area of a two-dimensional shape, you use a specific mathematical formula that depends on the type of shape. For example:
- For a rectangle, area = length × width ($A = l \times w$)
- For a triangle, area = 1/2 × base × height ($A = \frac{1}{2}b h$)
- For a circle, area = π × radius squared ($A = \pi r^2$)
2. How to find area of 3D shapes?
Although 3D shapes have volume, their surface area can be found by adding together the areas of all their two-dimensional faces. For instance:
- A cube's surface area: $A = 6a^2$, where $a$ is the length of one side
- A cylinder's surface area: $A = 2\pi r h + 2\pi r^2$, where $r$ is the radius and $h$ is the height
3. How to find the area of an irregular 2D shape?
To determine the area of an irregular 2D shape, you can:
- Divide the shape into regular geometric shapes (such as rectangles, triangles, circles), find each area, and sum them up
- Use grid paper or graphing methods by counting the number of enclosed squares
4. How to find the area and perimeter of 2D shapes?
Area measures the space inside a shape, and perimeter is the total distance around its edges. You can find these using standard formulas. For example:
- Rectangle:
- Area: $A = l \times w$
- Perimeter: $P = 2(l + w)$
- Circle:
- Area: $A = \pi r^2$
- Perimeter (Circumference): $C = 2\pi r$
5. What are the standard formulas for the area of common two-dimensional shapes?
The standard area formulas for common 2D shapes are:
- Square: $A = a^2$ (where $a$ is the side length)
- Rectangle: $A = l \times w$
- Triangle: $A = \frac{1}{2}bh$
- Parallelogram: $A = b \times h$
- Circle: $A = \pi r^2$
- Trapezium: $A = \frac{1}{2}(a + b)h$ where $a$ and $b$ are parallel sides, $h$ is height
6. Why is understanding the area of 2D shapes important in real life?
Understanding the area of 2D shapes is practical in daily life for:
- Calculating the amount of material needed (such as tiles, paint, carpet)
- Planning layouts (e.g., gardens, rooms or plots of land)
- Design and construction work
7. How can students practice area of 2D shapes problems effectively?
To practice problems on the area of 2D shapes effectively, students should:
- Solve exercises of increasing complexity
- Work with different shapes and mixed-question formats
- Utilize Vedantu’s interactive worksheets, quizzes, and doubt-solving sessions
8. What are some common mistakes when calculating the area of 2D figures?
Common mistakes include:
- Confusing area with perimeter
- Using incorrect units (e.g., cm instead of cm2)
- Applying the wrong formula for the given shape
- Calculation errors in multiplying or squaring numbers
9. How is the area of composite 2D shapes calculated?
The area of composite 2D shapes is calculated by breaking the figure into simpler shapes, finding the area of each part, and then adding (or subtracting, if necessary) the areas together. Vedantu specializes in teaching problem-solving strategies for such complex figures through diagrams and interactive sessions.
10. How can Vedantu support students in mastering the area of two-dimensional shapes?
Vedantu provides:
- Live classes with expert math teachers
- Interactive practice questions and quizzes
- Personalized doubt-clearing sessions
- Comprehensive study materials tailored to all curriculum levels





















